Teil 1: Das SEIR- und das SIR-Modellwie von Hethcote beschrieben
x λ, δ und γ sind Konstanten |
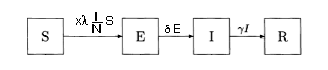
N = S + E + I + R = zeitlich konstant |

1 = s(x) + e(x) + i(x) + r(x) |
nach "The Mathematics of Infectious Diseases"
von Herbert W. Hethcote
SIAM Review, Vol. 42, No. 4. (Dec., 2000), pp. 599-653.
http://links.jstor.org/sici?sici=0036-1445%28200012%2942%3A4%3C599%3ATMOID%3E2.0.CO%3B2-Q
Hier liegt Material, das dabei helfen soll, Influenza mit Corona zu vergleichen.
Zusammenfassung
Mit dem SEIR- und dem SIR-Modell werde ich in (Teil 1) zeigen,
abhngt (Abb. 4 a - d).
Im Link hinter Abbildung 4e interpretiere ich den deutschen COVID-19-Verlauf im Jahr 2020 mit dem SIR-Modell. Dabei passe ich die Modellparameter so an, dass Teile des festgestellten Verlaufs vom SIR-Modell dargestellt werden.
In den Abbildungen 5 vom Teil 2 fhre ich als Erweiterung des SEIR-Modells das Superspreading-Modell vor. Es zeigt, wie die Corona-Pandemie mit Testen, Kontaktnachverfolgung und Isolation der infektisen Personen (TTI) eingedmmt werden kann. Die Arbeitsgruppe um Viola Priesemann in Gttingen gibt quantitative Hinweise, wie stark die infektisen Kontakte beschrnkt werden mssen, um die Pandemie soweit zurckzufahren, dass sie nicht wieder von selbst aufflammt.
Im Teil 3 (Beobachteter Pandemieverlauf) findet man in Abbildung 6 und 7a zum Vergleich der Modellvorstellungen mit der Wirklichkeit den Verlauf des 7-Tage-Mittels der tglichen beobachteten (PCR-positiven) Fallzahlen dargestellt. Wie in Abbildungen 1 und 4 habe die linear-logarithmische Darstellung gewhlt, weil man darin die Halbwertszeiten T in verschiedenen Stadien t0 der Pandemie besser erkennen kann. Sie zeigen sich in den Steigungen der geraden Abschnitte der Kurven. Aus den Halbwertszeiten mchte ich Aussagen ber die Effizienz des Lockdowns machen. Verringert sich die Steigung (vergr§ert sich T), dann haben die Menschen ihre Kontaktbeschrnkungen (social distancing) verstrkt, entweder absichtlich oder unabsichtlich, letzteres z.B. durch die Vernderung der Jahreszeit bedingt.
Abbildungen 7a bis 7c zeigen den Vergleich Deutschland - Schweden, und wenn man auf die Abbildungen klickt, sieht man den Vergleich zu allen EU-Lndern in einem Video.
Mit Hilfe des aus Teil 2 und 3 gewonnenen qualitativen Verstndnisses vom SIR Superspreading-Modell kann ich in Teil 4 Alexander Kekulés Kritik an den vergangenen und laufenden Corona-Ma§nahmen der Politik einordnen.
Teil 1: Das SEIR- und das SIR-Modellwie von Hethcote beschrieben
x λ, δ und γ sind Konstanten |

N = S + E + I + R = zeitlich konstant |

1 = s(x) + e(x) + i(x) + r(x) |
x = ein Ma§ fr die Weitergabe der Infektion, d.h.
N = Gesamtzahl der Menschen in der betrachteten, im Wesentlichen nach au§en abgeschlossenen (isolierten) Gruppe (population)
S(x), s(x) = Anzahl bzw. Bevlkerungsanteil (S(x)/N) der noch nicht infizierten Menschen (the susceptibles)
E(x), e(x) = Anzahl bzw. Bevlkerungsanteil (E(x)/N) der angesteckten Menschen in der Latenzzeit, d.h. bevor sie Symptome haben und ansteckend wirken (the exposeds)
I(x), I(x) = Anzahl bzw. Bevlkerungsanteil (I(x)/N) der Menschen, die ansteckend wirken (the infectious)
R(x), r(x) = Anzahl bzw. Bevlkerungsanteil (R(x)/N) der gesundeten (recovered) oder gestorbenen Menschen
λ = Kontaktrate, mit der ein einzelner Mensch die Krankheit weitergibt (Ansteckungsrate, Infektionsrate)
γ = pro-Kopf "Genesungs"rate
Die Ansteckung wchst und fllt mit dem Bruchteil i = I/N der ansteckenden Menschen (I/N = i steht in der Differentialgleichung fr S), und damit ist das System nichtlinear.
Verwendete Parameter
Abgeleitete Parameter
Typisch fr das SEIR-Modell ist die "Herd Immunity Threshold" (HIT = 1 / σ): Wenn s(t) den Wert HIT unterschreitet, klingt die Pandemie ab, sie hat ihre Sttigungsgrenze erreicht. Von diesem Punkt an fllt der Bruchteil der infektisen Menschen i(t). In Abbildungen 1 bis Abbildungen 3 wird die HIT abhngig von der Basisreproduktionszahl R0 zwischen 3 und 7 Tagen erreicht. Das ist wesentlich frher als bei der COVID-19-Pandemie).
|
Abb. 2a: Am Lockdown bei Zeit 1.5 Tage (senkrechte Linie) ndert sich σ (= R0) von 4.0 nach 3.2 (entspr. x λ von 1.0 / d nach 0.8 / d). Die punktierten Kurven stellen die um den Faktor 10 vergr§erten entsprechenden halbtglichen Neuinfektionen nF(t) dar:
Die im Bereich 0 bis 6 Tage hheren Kurven fr e(t), i(t), r(t) und nF(t) gehren zu σ = 4, die entsprechenden niedrigeren Kurven gehren zu σ = 3.2. Die Zuordnung von σ zu den Kurven s(t) ist umgekehrt.
Bei σ = R0 = 3.2 ist das Maximum der tglich neu infizierten Personen
Beachten: im Gegensatz zu Abbildung 1 ist die Ordinate hier linear geeicht. |
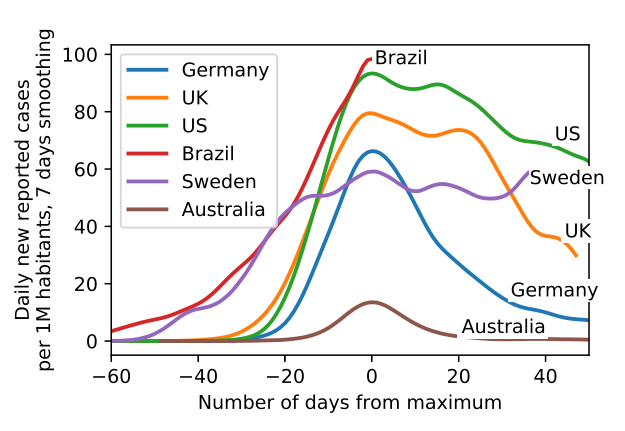
Abb. 2b (literatur/priesemann/priesemann_2020.png): Comparison of the daily case numbers per one million inhabitants of exemplary countries as illustration of the range of possible case numbers developments. Note how both the peak height as well as peak width of some countries are considerably larger than for Germany, providing evidence against saturation effects ("herd immunity") in Germany (Data until June 3, 2020)
Quelle: Fig. 7 of Dehning, J et al., Model-based and model-free characterization of epidemic outbreaks, Sept. 18, 2020.
|

Abb. 3a: Herdenimmunitt im SEIR-Modell. Herdenimmunitt (HIT, Punkte bei s(t) = γ / (x λ)) bei einer Basisreproduktionszahl R0 ist erreicht, wenn die entsprechende Kurve nach unten abbiegt. Lockdowns derselben Strken und zur selben Zeit wie in Abbildungen 1 und 2. Statt des zeitlichen Verlaufs (Abbildungenen 1 und 2) ist hier i(t) gegen s(t) aufgetragen. Die Pfeile zeigen in Richtung ansteigender Zeit t. |

Abb. 3b: Herdenimmunitt im SIR-Modell. Herdenimmunitt (HIT, Punkte bei s(t) = γ / (x λ)) bei einer Basisreproduktionszahl R0 ist erreicht, wenn die entsprechende Kurve nach unten abbiegt. Lockdowns derselben Strken und zur selben Zeit wie in Abbildungen 1 und 2. Statt des zeitlichen Verlaufs (Abbildungen 1 und 2) ist hier i(t) gegen s(t) aufgetragen. Die Pfeile zeigen in Richtung ansteigender Zeit t. |
|
Abb. 4c: Einfluss der Kontaktzahl σ = R0 = γ / xλ auf den Pandemieverlauf. Die Zahlen an den Kurven geben σ an.
Die Kurven stellen die Paare s(t) und i(t) als Funktion der Zeit t dar. Alle Kurvenpaare starten bei ihrer Anfangsbedingung s(t=1) = 0.95, i(t=1) = 0.05. Das Kurvenpaar zu σ = 3.2 ist identisch mit dem Kurvenpaar zum anfnglichen Bruchteil i(t=1) = 0.05 in Abbildung 4a.
Je hher die Kontaktzahl σ ist, desto frher und hher liegt das Maximum von i(t), an dem die Bevkerung ihre Herdenimmunitt erreicht (Herdenimmunitt tritt beim Maximum von i(t) ein).
Auf Abbildung klicken, um in einem Videoclip die 5 Kurvenpaare {s(t), i(t)} einzeln zu sehen.
|
Abb. 4d: Pandemieverlauf und Parameter wie in Abbildung 4c, jetzt aber im Phasenraum veranschaulicht: Die Kurven stellen i(t) als Funktion von s(t) dar. Die Zahlen an den Kurven geben σ an. Jede Kurve startet rechts bei ihrer Anfangsbedingung s(t=1) = 0.95, i(t=1) = 0.05. Das Kurvenpaar zu σ = 3.2 ist identisch mit dem Kurvenpaar zum anfnglichen Bruchteil i(t=1) = 0.05 in Abbildung 4b.
Je hher die Kontaktzahl σ ist, desto strker wird die Bevkerung infiziert, bis ihre Herdenimmunitt eintritt (Herdenimmunitt tritt beim Maximum von i(t) ein).
Auf Abbildung klicken, um in einem Videoclip jede Kurve einzeln zu sehen. |
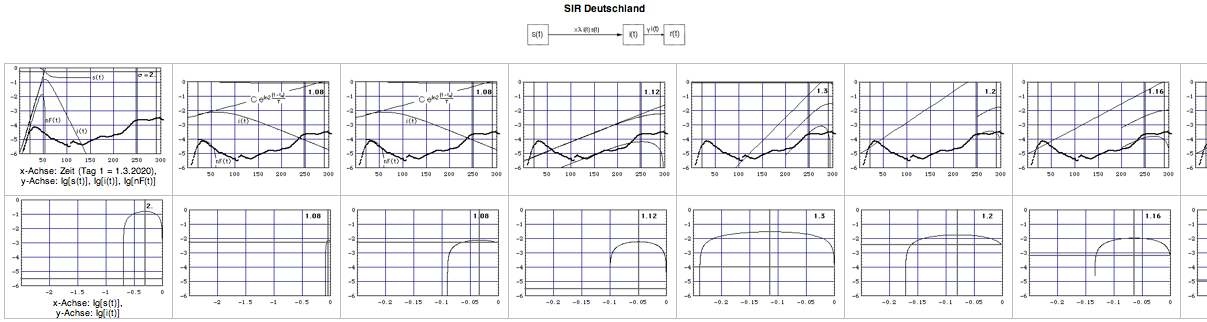 Abb. 4e. Dynamik der COVID-19-Pandemie in Deutschland zu ausgewhlten Zeitpunkten. zum Vergr§ern auf Bild klicken |
Teil 2: SEIR Superspreading-Modelle von G. Gomes et al. und V. Priesemann et al.x λ, δ und γ folgen kontinuierlichen Verteilungen |
Fr das SEIR- oder SIR-Modell mit konstantem x ist die lawinenartige Pandemieausbreitung charakteristisch (gerade Kurvenstcke in Abbildung 1 bis zur HIT). Die Abbildung 7 von Dehning et al. zeigt, dass die Rate x λ (die den exponentiellen Anstieg der Kurven mitbestimmt) von Gesellschaft zu Gesellschaft variiert.
berdies besteht die Bevlkerung eines Landes (in guter Nherung) aus Subpopulationen mit verschiedenen x λs, die nur schwachen infektisen Kontakt miteinander haben. Die Pandemieentwicklung ist also in guter Nherung eine berlagerung der Kurven zu verschiedenen x λs in den Abbildungen 3. Die HIT dieser berlagerung liegt niedriger als die HIT des Systems mit dem gr§ten x λ und kommt so der beobachteten Pandemieentwicklung nher. Darauf baut das SEIR- oder SIR-Superspreading-Modell auf.
Diesen Teil kann ich nicht modellieren. Ich hoffe, dass mein im Folgenden beschriebenes qualititatives Verstndnis zutrifft.
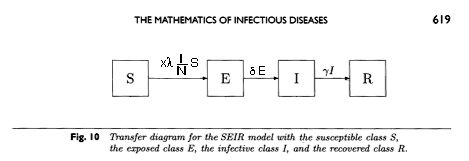
Wenn x nicht einfach eine feste Konstante ist, sondern einer (Normal-, Lognormal- oder Gamma-) Verteilung folgt, beschreibt das SEIR-Modell einen neuen Infektionsausbreitungsvorgang, das "Superspreading": Die Infektion wird nicht gleicherma§en von allen Infektisen weitergetragen, sondern von nur wenigen. Die restlichen Infektionsketten enden rasch. Das gibt der Pandemiebekmpfung die Chance, solche Superspreading-Vorgnge zu lokalisieren und durch gezielte Kontaktbegrenzungen einzudmmen (test-trace-and-isolate, TTI).
"TTI-Ma§nahmen liefern einen wichtigen Beitrag zur Pandemiekontrolle, aber allein reichen sie typischerweise nicht aus. Ihr Erfolg hngt stark von ihrer Umsetzung ab:
Im Rahmen unserer informierten Festlegung der [Fit-]Parameter zeigt unser [Superspreading-]Modell, dass Reduktion der infektisen Kontakte und TTI die Pandemie nur bis zu einer Basisreproduktionszahl R0 = 3.3 eindmmen knnen, wenn die [infektisen] Kontakte um etwa 40% reduziert werden." (Contreras et al. 2020, Exzerpt)
 .png)   mu = 1, beta = 1 |
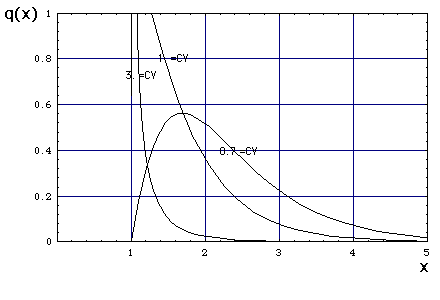
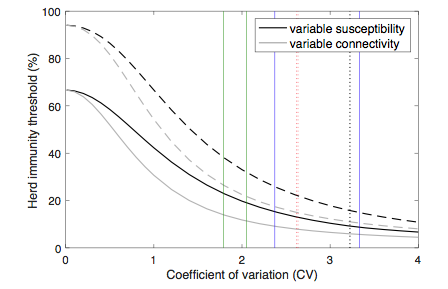 Figure 3 von Gomes et al.: Herd immunity threshold with various distributions q(x) of susceptibility x or exposure x to infection (connectivity). Curves generated with the model (Equation 1) with gamma distributed susceptibility (black) or connectivity (gray) q(x) assuming R0 = 3: (solid) herd immunity threshold (HIT); (dashed) final size of uncontrolled epidemic.
|
|
Abb. 5a: Gamma-Verteilung von x. Beachten: Der hier verwendete Parameter γ ist nicht zu verwechseln mit dem γ des SEIR-Modells, der bergangsrate vom Kompartment I zum Kompartment R (oben). |
Abb. 5b: Das charakteristische Verhalten des SEIR-Modells bei kontinuierlich verteiltem x (Abb. 5a): Herdenimmunitt wird umso frher erreicht, je enger die Verteilung von x ist (je gr§er der Coefficient of Variation CV ist). Bei enger Verteilung q(x) (gro§em CV) bleibt ein betrchtlicher Teil der Bevlkerung von der Pandemie verschont, weil die Infektion nicht explosionsartig um sich greift, sondern sich auf eng begrenzte Bevlkerungsbereiche beschrnkt. |
Interpretation
Der mit einem Superspreading-Modell beschriebene Ablauf der Pandemie gleicht dem In-Brand-Geraten und Brennen eines Packens von Papierbndeln (Gesellschaftsgruppen, innerhalb derer Superspreading abluft, deren Au§enkontakte aber pandemisch kaum infektis sind), das einem Funkenflug (der Infektion) ausgesetzt ist.
Most frequently we were asked if and in what sense our results have a causal interpretation. As we will explain [in this paper] below, our approach selects the most plausible of multiple causal explanations of the observed data, but does not establish strict interventional causality."
Quelle: Dehning, J. et al., "Model-based and model-free characterization of epidemic outbreaks", Sept. 16, 2020
Teil 3: Beobachteter Pandemieverlauf |
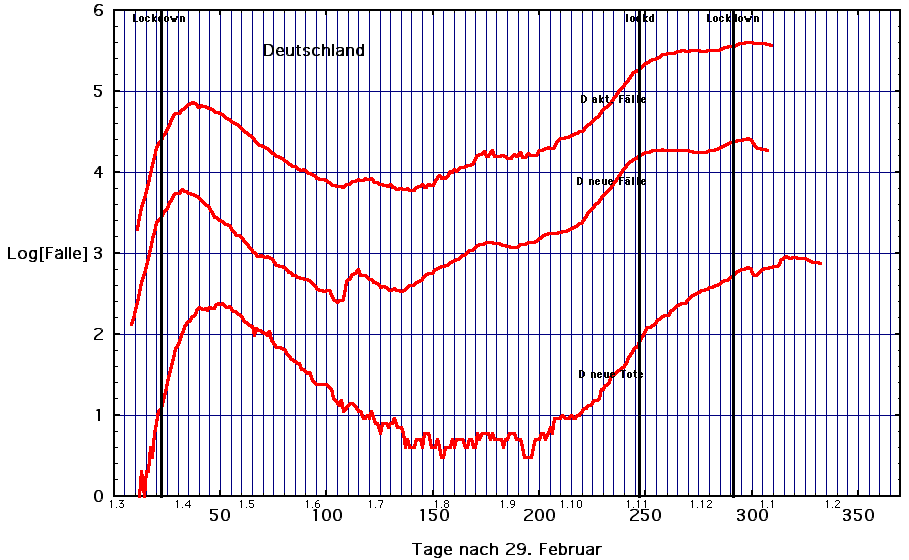
Abb. 6: Corona-Statistik nach worldometers.info:
Die senkrechten Linien haben einen 5-Tage-Abstand. Die Ordinate ist wie in den beiden folgenden Abbildungen der 10er Logarithmus der Fallzahlen.
Ich habe nicht verstanden, wie die aktiven Flle berechnet werden. worldometers.info verweist auf Schtzungen des Berliner Tagesspiegels.
Abb. 7a: Corona-Statistik der 7-Tage-Inzidenz (= Anzahl der Flle innerhalb von 7 Tagen pro 100 000 Personen) nach Tagesspiegel: Vergleich Deutschland - Schweden. Ordinate ist logarithmisch geeicht.
Auf Graphik klicken, um Vergleich mit allen EU-Lndern zu sehen.
Linear-logarithmische Darstellung der Fallzahlen.
In linear-logarithmischer Darstellung sind
teilweise aus Geradenstcken zusammengesetzte Kurven. Die Geraden zu (a) und (b) verlaufen parallel zueinander. Der zeitlichen Anstieg der Geraden ist ein Abbild des Differentialgleichungssystems (im einfachsten Fall dem obigen Modell, aber auch demdetaillierteren Modell von Viola Priesemann et al., das social distancing und infectivity explizit trennt). Aus dem zeitlichen Anstieg der Kurven mchte ich auf die tatschlich verwirklichten social distancing Ma§nahmen schlie§en.
Es gibt in Abbildung 6a Zeitintervalle, in denen die Kurvenstcke von vielen Lndern weitgehend parallel verlaufen, also die Kombinationen infectivity - social distancing von Land zu Land kaum variiert. Die verschiedenen Hhen, in denen die Kurvenstcke liegen, spiegeln in Abbildung 6 verschiedene Populationsgr§e und Infektionsdruck, in Abbildung 7a allein den verschiedenen Infektionsdruck wider. mehr dazu.
Abb. 7b: Corona-Statistik der tglich neuen Todesflle nach Tagesspiegel: Vergleich Deutschland - Schweden. Ordinate ist logarithmisch geeicht.
Auf Graphik clicken, um Vergleich mit allen EU-Lndern zu sehen.
Abb. 7c: Corona-Statistik der kumulativen Todesflle nach Tagesspiegel: Vergleich Deutschland - Schweden. Ordinate ist linear geeicht.
Auf Graphik clicken, um Vergleich mit allen EU-Lndern zu sehen.
Die Anstiege und Abflle spiegeln wider, wie sich die Bevlkerung an die Shutdown-Auflagen hlt: im Herbst/Winter 2020/21 hlt sie sich jahreszeitlich bedingt weniger daran als im Frhjahr 2020, wo die Pandemie in die warme Jahreszeit hinein lief, in der die aerogene bertragung abnahm.
"Ich glaube, wir mssen lernen, dass der offene wissenschaftliche Diskurs wichtig ist und dass man gro§e Gremien von Wissenschaftlern braucht, die miteinander diskutieren. Wenn man die immer nur einzeln fragt, ist das schlecht. Man braucht ein Gremium, denn das Ergebnis von solchen Gremien ist meistens besser. Und vor allem, wenn die Politiker dabeisitzen und sich das anhren, verstehen die ja auch ein bisschen die Argumente besser. Ich glaube, das htten wir am Anfang unbedingt machen mssen. Das steht brigens in den Pandemieplnen, dass man dafr eine Kommission, eine Fachkommission grnden soll. Das ist nicht gemacht worden und wie viele Punkte in der Schublade geblieben."
Teil 4: Kritik an den Corona-Ma§nahmen - Alexander Kekul und Lisa FederleDie Abbildungen habe ich eingefgt. Alexander Kekulé hat keinen Bezug darauf genommen. |
|
Kekules Corona-Kompass Transkripts #83 - #252
|
|
[Das] sind die Haupttreiber [der Infektion]:
|
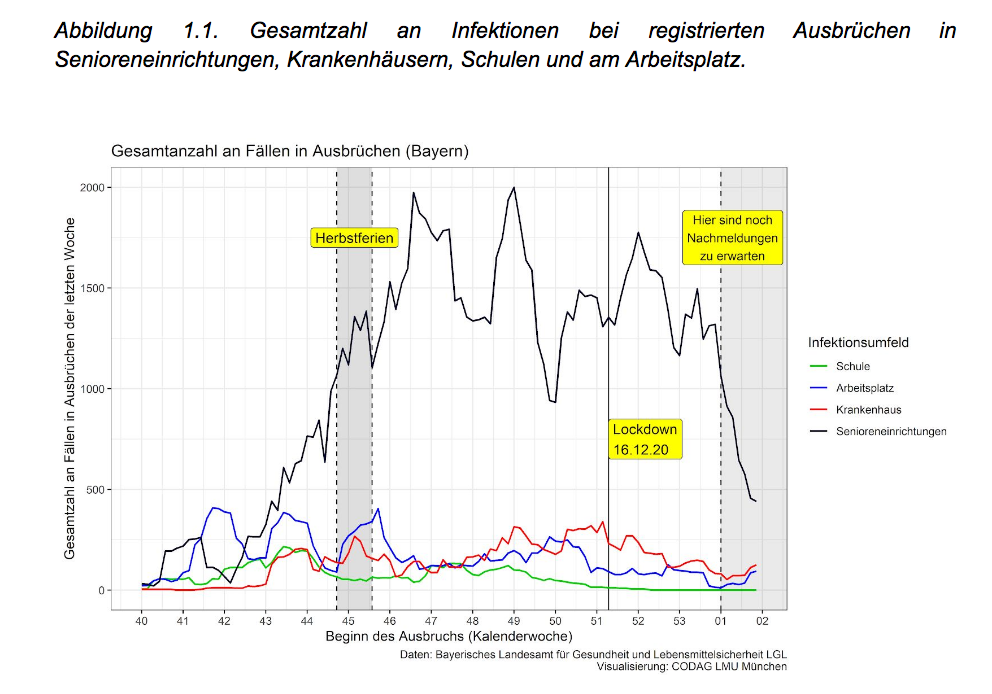
Als Ausbruch wird ... eine Hufung von mindestens zwei Infektionen bezeichnet, die epidemiologisch miteinander in Verbindung stehen. Abbildung 1.1. zeigt die Gesamtzahl an Fllen dieser Ausbrche zum jeweiligen Tag der ersten Meldung, der den Beginn des Ausbruchs definiert. Das hei§t, die Kurven geben jeweils alle Flle in einem Ausbruch zu Beginn des Ausbruchs wieder.
Quelle: Abbildung 1.1 in Bericht 8, 5.2.2021, CODAG, LMU Mnchen (im Cache)
siehe auch Aufschlsselung nach Altersgruppen und Bundeslndern in Abbildung 4 in Bericht 5, 22.12.2020, CODAG, LMU Mnchen (im Cache) |
"Auch wenn man die meisten Infektionen nicht mehr nachvollziehen kann, wissen wir, das ist im Moment das Problem. Da widerspricht niemand. Deshalb htte ich mir gewnscht, dass man dort strker eingreift. Das hat man aber nicht gemacht, stattdessen alle bedacht.
Das ist so hnlich, als wenn Sie sagen, ich will ein Parkproblem in der Innenstadt lsen. Es gibt zu viele Autos.
Ich htte mir gewnscht, dass man die Falschparker abschleppt und die Strafzettel konsequenter verteilt und dann mal sieht, ob das nicht vielleicht schon reicht, um das Problem zu beheben."
Quelle: Kekuls Corona Kompass #115 , audio, im Cache)
mehr dazu von Alexander Kekulé
|
"Teilweise gibt es schon Regionen in Deutschland, die in einem komfortablen Bereich angekommen sind. Dann sagt man, okay, jetzt ffnen wir mal die Friseure. Ich bin nicht dafr, dass man einfach irgendwie aufmacht. Weil alle Lnder, die in der jetzigen Situation oder in hnlichen Situationen geffnet haben, das dann damit bezahlen mussten, dass die Fallzahlen wieder dramatisch angestiegen sind. Gerade so um Weihnachten rum hatte man in Irland, England und anderen Teilen der Welt auch diese Probleme. Dieser Ausbruch in Portugal war ja im Grunde genommen auch die Konsequenz einer ffnung.
Das sind immer unkontrollierte ffnungen gewesen. Es hat keinen Sinn, "Schleuse zu, Schleuse auf" zu denken. Sondern man muss berlegen, wie kann man diesen Lockdown, der immer irgendwie wirken muss, durch selektivere, intelligentere Ma§nahmen ersetzen. Das muss man natrlich auch vorbereiten. Es tut mir leid, das zu sagen, weil wir schon fast ein ganzes Jahr ber dieses Thema sprechen in diesem Podcast. Ich sehe da noch nicht so richtig eine Strategie. Wie kommt man Schritt fr Schritt raus?
Vorschlge fr kontrollierte ffnungen:
Quelle: Kekulés Corona Kompass #148 Ê |
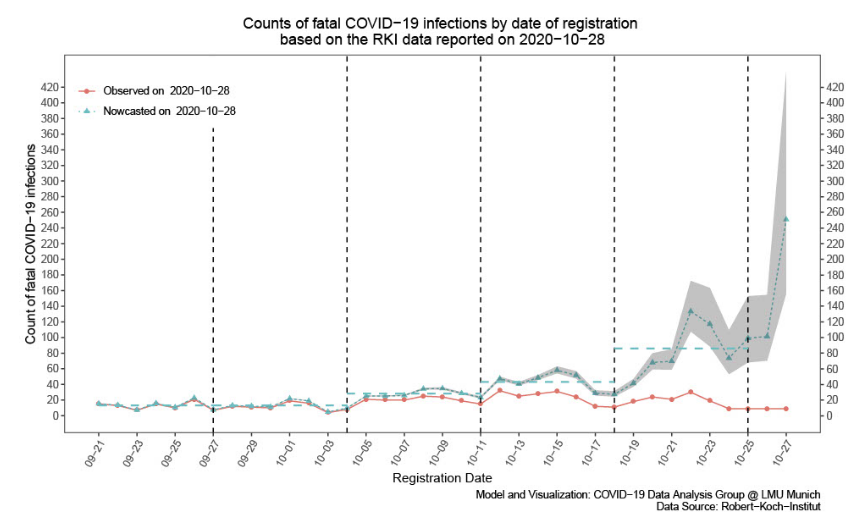
Quelle: Bericht 1, 30.10.2020, CODAG, LMU Mnchen (im Cache) |
|
Camillo Schumann
Wenn Sie diese Zahlen hren, was sagen Sie dazu?
Quelle: Kekuls Corona-Kompass #124, audio |
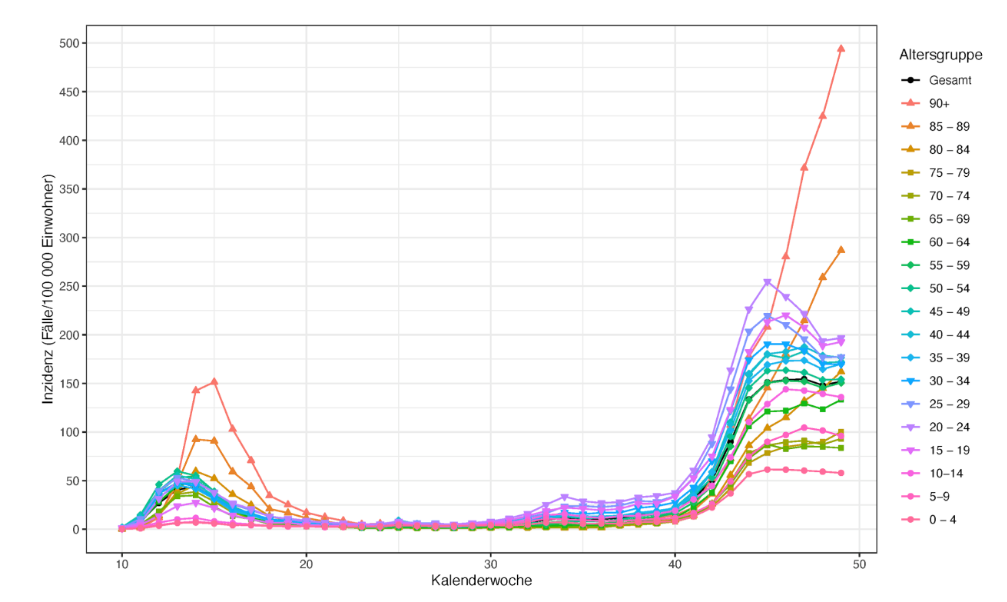 Die Einschrnkungen des ffentlichen Lebens haben dazu beigetragen, dass die Anzahl der Neuinfektionen rcklufig ist, allerdings nicht fr die ltesten. Abbildung 6 zeigt die Anzahl der Neuinfektionen pro 100.000 Einwohner in unterschiedlichen Altersgruppen. Man erkennt fr alle Altersgruppen einen steilen Anstieg bis zur Kalenderwoche 45. Danach flacht sich dieser Anstieg fr fast alle Altersgruppen ab und die Infektionszahlen reduzieren sich. Insbesondere fr die Altersgruppe der 20 -24-Jhrigen zeigt sich ein Rckgang. Dies zeigt empirisch, dass die ergriffenen Ma§nahmen das Infektionsgeschehen in Deutschland teilweise eindmmen konnten. Dies gilt allerdings nicht fr die ber 85-Jhrigen. Hier ist der Anstieg der Infizierten ungebrochen und steigt auch weiterhin an; besonders steil bei den ber 90-Jhrigen.
Quelle: Abbildung 5 in Bericht Nr. 4, 11.12.2020, CODAG, LMU Mnchen(im Cache) |
Wie wir COVID-19 unter Kontrolle bekommen (BMI-Link)
Paul Cullen, Brigitte Knig, Jens Schwachtje, Henrieke Stahl, Henrik Ullrich, Berliner Zeitung, 15.01.2024
(im Cache)
Konsensuelles Ð mit Sprengkraft fr die Diskussion
(2) Es besteht Konsens, dass das Spikeprotein Ð egal ob im Virus oder als Ergebnis der
modRNA-Injektion gebildet Ð schdlich sein kann. Es kann fr schwere Covid-Verlufe sowie
das post acute covid syndrome (PACS, ãlong-CovidÒ) oder aber auch das post acute covid
vaccination syndrome (PACVS, ãpost-VaxÒ) Ð zusammen auch mit anderen Faktoren Ð
verantwortlich sein.
In Studien wurden Zusammenhnge zwischen dem modRNA-Wirkprinzip und dem durch die
modRNA gebildeten Spike-Protein mit bestimmten Erkrankungen gefunden, darunter
Herzmuskelentzndungen, Gerinnungsstrungen und das myalgische Enzephalitis/chronische
Mdigkeitssyndrom (ME/CSF). Die Frage, welches Gewicht dem Spike-Protein in Relation zu
den anderen Proteinen des Coronavirus fr seine Pathogenitt zukommt ist weiterhin Gegenstand
der wissenschaftlichen Diskussion.
(3) Es gilt als gesichert, dass nach Impfung Spikeproteine deutlich lnger im Krper gebildet werden als anfangs gedacht bzw. geplant war. So wurden sie in Lymphknoten 60 Tage und in anderen Geweben vier bis sechs Monate nach Impfung nachgewiesen. Auch besteht Konsens, dass diese Persistenz das Risiko fr Nebenwirkungen erhht.
(4) Ebenso ist wissenschaftlich gesichert, dass der Impf-Wirkstoff nicht, wie immer noch gern in
Medien kommuniziert wird, an der Injektionsstelle im Arm verbleibt, sondern sich breit verteilt,
die Blut-Hirn- sowie Plazenta-Schranke berwindet und in der Muttermilch erscheint. Zellen
verschiedener Gewebe exprimieren das Spike-Protein, so dass diese zum Angriffspunkt fr das
Immunsystem werden knnen.
Einigkeit besteht ferner darber, dass die Lipidnanopartikel, in denen die modRNA verpackt
wird, selbst schdlich wirken knnen, etwa Entzndungen auslsen.
(5) Dass eine Studie mittels ãcomputergesttzter VerfahrenÒ eine mgliche Interaktion des Spikes mit einem Krebs-assoziierten Protein gezeigt hat, ist unstrittig. Gegen die Behauptungen in Harmsens Artikel, es gebe keine Hinweise auf einen Zusammenhang von Krebs und Covid-19- Impfung und es sei ãunplausibelÒ, dass Spike Krebs begnstigen oder auslsen knne, sprechen jedoch sowohl statistische Befunde als auch erste pathophysiologische und andere Studien.
(6) Bei der Massenherstellung der modRNA-Impfstoffe mittels Escherichia coli-Bakterien kommt es trotz entsprechender Reinigungsma§nahmen zu einer Kontamination mit DNA- Fragmenten, die in die Lipidnanopartikel eingeschlossen und somit in das Zellinnere transportiert werden knnen. Unter bestimmten Bedingungen knnen diese DNA-Reste bis in den Zellkern vordringen. Welche tatschlichen Auswirkungen diese Verunreinigungen in der Zelle und gegebenenfalls im Zellkern haben, ist unbekannt. Jedenfalls aber ist hier ein Potenzial fr mgliche Krebsursachen vorhanden.
In seinem Podcast hat Professor Kekul zu diesem Sachverhalt gefragt, weshalb Hersteller und Behrden ãnicht mal mit klaren Statements reagierenÒ. Das hat das Paul-Ehrlich-Institut am 22. Dezember 2023 mit einem Informationsschreiben getan. Das Papier besttigt die DNA- Verunreinigung, behauptet aber, diese sei unschdlich, weil die Menge gering und die DNA- Fragmente kurz seien. Daten, die diese Behauptung gesicherter Unschdlichkeit im Fall der Covid-19-modRNA-Impfstoffe mit ihrer oben geschilderten neuartigen Spezifik sttzen wrden, existieren nach unserem Wissen nicht.
Auch wird in diesem Schreiben au§er Acht gelassen, dass die gefundene Menge an DNA- Verunreinigung stark von der Messmethode abhngt. Die qPCR-Technik, die wir auch von der SARS-CoV2-Diagnostik kennen, findet nur einzelne Gensequenzen, die man vorher definiert hat. Alle anderen Sequenzen werden unabhngig von ihrer Menge einfach bersehen. Daher ist die qPCR zur Gesamt-DNA-Bestimmung ungeeignet, wird aber von den Herstellern Ð in bereinstimmung mit der EMA Ð dennoch hierfr verwendet.
Es fragt sich, weshalb nicht Methoden genutzt werden, die sich zur Bestimmung des DNA- Gesamtgehalts eignen, zumal den Herstellern die Problematik einer Untererfassung der DNA bewusst ist. So legt ein Patent von Moderna (US 10 ,077 ,439 B2, Spalte 19) zur ãEntfernung von DNA im mRNA-ProduktionsprozessÒ dieses Problem explizit dar: ãDie quantitative PCR wird hufig zur Messung der Rest-DNA eingesetzt, aber sie erfasst nur die DNA-Molekle, die beide qPCR-Primer enthalten, und misst daher nicht alle anderen kleineren DNA-Molekle, die teilweise verdaut sind.Ò Im Patent wird deshalb zur Messung von Rest-DNA eine hochempfindliche physikalische Messmethode (Flssigchromatographie-Tandem- Massenspektrometrie) empfohlen. Fr die Covid-19-modRNA-Impfstoffe wird jedoch diese Empfehlung nicht bercksichtigt.
Wir drfen nicht vergessen, dass es sich bei den modRNA-Produkten der Sache nach um Gentherapeutika handelt, die nur mittels einer âjuristischen FiktionÔ aus dieser Kategorie ausgenommen und daher bei ihrer Zulassung weder auf krebserregende noch auf genotoxische Wirkungen hin untersucht wurden.
Die Lnge dieser Liste von bereinstimmungen in Bezug auf problematische Aspekte der Spikeproteine und der modRNA-Covid-19-Impfstoffe, auch wenn ihre Einschtzung im Detail divergiert, untermauert den Bedarf zur Vertiefung der Forschung und zu einer Ausweitung der ffentlichen Debatte zur Sicherheit dieser Impfstoffe. Es fragt sich, weshalb in den Leitmedien zu diesen Fragen nicht schon frher eine Diskussion begonnen wurde.
Dissens im Diskurs
Wie in einem wissenschaftlichen Diskurs zu erwarten, waren die von Herrn Harmsen konsultierten Kollegen nicht mit all unseren Schlussfolgerungen einverstanden:
(1) Einige Kollegen teilen unsere Hypothese nicht, dass durch die Injektion das Spike gefhrlicher als nach der Infektion werden knne. Sie bezweifeln, dass sich das Spike nach einer Impfung im Krper mehr anreichert als nach einer Infektion.
Richtig ist, dass bisher unklar ist, wieviel Spike typischerweise nach Impfung im Krper gebildet wird, und inwieweit diese Menge von der Impfdosis und von der geimpften Person selbst abhngt. Auch die Viruslast schwankt erheblich je nach Schweregrad der Infektion. Dazu kommen noch die Unterschiede der Virusvarianten sowie die Mglichkeit, dass das Spike-Protein im Viruskomplex anders wirkt, als wenn es in Reinform nach der Impfung vom Krper gebildet wird.
Unsere These einer erhhten Schdlichkeit der Covid-19-Impfung im Vergleich zur Infektion beruht auf der Annahme, dass durch die Impfung das Spike zwangslufig ins Krperinnere gelangt bzw. dort hergestellt wird, whrend das Virus hierfr erst verschiedene Immunschranken berwinden muss und sich nur bei verhltnism§ig seltenen schweren Krankheitsverlufen in einem relevanten Ausma§ systemisch ausbreitet bzw. vermehrt.
Zu diesen Fragen besteht erheblicher Forschungsbedarf.
(2) Es wird die Ansicht vertreten, die Verwendung von N1-methyl-Pseudouridin in der Impf- modRNA sei ungefhrlich. Dieses Pseudouridin werde nicht wie ãnormaleÒ RNA-Bausteine wiederverwendet, sondern, wie Herr Kekul in seinem Podcast berichtet, nach Abbau der modRNA direkt ausgeschieden. Eine dadurch erhhte Gefhrdung des menschlichen Krpers bestehe deshalb nicht.
Die Wirkung und Verstoffwechselung der modRNA und des darin enthaltenen Pseudouridins ist aber ein hochkomplexes Thema mit vielen offenen Fragen. Zum Beispiel zeigt eine am 13. Dezember 2023 erschienene Studie in der renommierten Fachzeitschrift Nature, dass das Pseudouridin in der modRNA zu Fehlern bei der Eiwei§herstellung in unseren Zellen fhrt, so dass nicht nur Spike-Protein, sondern auch eine signifikante Menge an nicht gewollten und nicht charakterisierbaren Eiwei§-Nebenprodukten gebildet wird. Welche Wirkungen diese Eiwei§- Nebenprodukte haben, ist unbekannt.
(3) In seinem Artikel zitiert Herr Harmsen die Virologin Prof. Ulrike Protzer, die unter Bezugnahme auf eine Studie behauptete, das Risiko einer Herzmuskelentzndung bei einer Covid-19-Erkrankung sei fnf- bis zehnmal hher als nach Impfung. Diese Studie (Patone et al. 2022) zeigt jedoch auch, dass bei unter-40-Jhrigen das Risiko einer Herzmuskelentzndung nach der zweiten Injektion mit dem Moderna-Produkt etwa 50% hher war als nach einer SARS- CoV-2-Infektion. Diese Studie wurde in der Zeit vor dem Auftauchen der weniger virulenten Omikron-Variante durchgefhrt. Solche relativierenden Faktoren, wie Alter und Pathogenitt der Virusvariante sowie ferner auch die Geschlechtsabhngigkeit dieser Komplikation (vgl. Buergin et al. 2023) mssen bercksichtigt werden.
In ihrer Gebrauchsinformation berichtet Pfizer selbst von einem ãerhhten MyokarditisrisikoÒ fr Kinder und Jugendliche, whrend die Herzmuskelentzndung fr Erwachsene als ãsehr selteneÒ Nebenwirkung (1:10.000) kategorisiert wird. Es existieren jedoch Hinweise, dass das Risiko einer impfinduzierten Herzmuskelentzndung deutlich hher ausfallen knnte, als bisher angenommen. In einer Studie zeigten alle Geimpfte, auch solche ohne Symptome, in der Zeit bis 180 Tage nach der Impfung bei Untersuchung mit einer empfindlichen nuklearmedizinischen Methode diskrete Vernderung des Stoffwechsels der Herzmuskelzellen, die auf ein hheres Risiko fr sptere krankhafte Herzmuskelvernderungen hinweisen knnten. Zudem gibt es auch keinen Konsens darber, wie gro§ das Risiko nach einer ãberstandenenÒ Herzmuskelentzndung fr sptere Herzschden ist.
(4) Der Marburger Kardiologe Bernhard Schieffer bezweifelt laut Harmsen unsere These, dass viele ãLong-CovidÒ-Flle in Wahrheit Post-Vax sind, denn hierfr fehle die wissenschaftliche Basis. In der Forschung wird diese Frage kontrovers diskutiert. Eine aktuelle Studie kommt zu dem Ergebnis, die Impfung reduziere das Risiko fr Long Covid. Jedoch leidet diese Studie, wie Professor Boris Kotchoubey gezeigt hat, an einem methodischen Defizit: Sie vergleiche gewisserma§en ãpfel mit BirnenÒ, denn sie differenziere nicht zwischen Menschen, die sich in der Zeit vor der Verfgbarkeit einer Covid-19-Impfung mit den frheren, als schwerer geltenden Virusvarianten infizierten, und Menschen, die sich whrend der Impfkampagne mit milden Virusvarianten angesteckt haben.
Zur Klrung der relativen Hufigkeit von Post-Covid und Post-Vax knnte eine Kohortenstudie beitragen, welche die unterschiedlichen Kombinationen von Infektionen, Virusvarianten und Impfungen sauber bercksichtigt. Der Goldstandard fr solche Vergleiche ist aber die klassische randomisierte prospektive Doppelblindstudie mit einer hohen Probandenzahl. In Folge der Durchimpfung der Kontrollgruppe der Pfizer-Zulassungsstudie nach nur sechs Monaten und der Durchimpfung eines gro§en Teils der Bevlkerung ist eine solche Studie jedoch kaum mehr mglich.
Das ist aus unserer Sicht eines der fundamentalen Probleme fr eine solide Einschtzung der Sicherheit der Impfstoffe. Denn hierfr fehlt genau die Datengrundlage, die bisher bei Impfstoffen mit Studien nach dem o.g. ãGoldstandardÒ erhoben wurde bzw. bisher behrdlich vorgeschrieben erhoben werden musste. Spter durchgefhrte retrospektive Fall-Kontroll-Studien fhren leicht zu Fehlinterpretationen in Bezug auf die Sicherheit der Impfstoffe. Selbst wenn sie die Gesamtsterblichkeit oder die Gesamterkrankung bercksichtigen, knnen sogenannte ãconfounding factorsÒ (Strfaktoren) das Ergebnis verflschen.
Deshalb knnen sie niemals prospektive randomisierte doppelblinde kontrollierte Studien ersetzen, in denen die Patienten per Zufall den Gruppen zugeteilt werden. Dies ist auch der Grund, warum die Durchimpfung der Kontrollgruppen in den Impf-Zulassungsstudien ein grober Versto§ gegen alle wissenschaftlichen Standards war. Die Hersteller beriefen sich fr diesen Schritt auf die Empfehlung, welche kurz zuvor die Weltgesundheitsorganisation (WHO) herausgegeben hatte. Die WHO behauptete, dass angesichts der Pandemiesituation die ethische Notwendigkeit bestehe, den Teilnehmern der Placebogruppe das Verum anzubieten. Nahezu smtliche Teilnehmer der Placebogruppen nahmen das Angebot an.
Offene Fragen
Die von Michael Andrick angesto§ene Debatte, ob und in welchem Ausma§ die beobachtete bersterblichkeit in einem Zusammenhang mit den Covid-19-Impfstoffen steht, hat die Risiken dieser Stoffe ins Licht der
ffentlichkeit gerckt. Sie zeigt aber auch, wie gro§ der Forschungsbedarf rund um die modRNA-Covid-19-Impfung ist. Und nicht zuletzt appelliert sie daran, die Debatte auch in den Medien sachlich, unter Bercksichtigung der Bandbreite der Forschung sowie auch der Reflexion ggf. methodischer Begrenzungen oder auch Defizite der Studien zu fhren. Argumente mssen frei und vorbehaltlos ausgetauscht werden knnen.
Fr uns ist ein wichtiges Ergebnis dieser Debatte, dass sie einige offene Fragen zur modRNA- Impftechnologie sowie zur Rolle des Spikeproteins auch fr ein breiteres Publikum in den Fokus gerckt hat.
Folgende Schlsselfragen ergeben sich aus der bisher gefhrten Kontroverse:
(1) Welches Gewicht kommt dem Spikeprotein im Rahmen des Krankheitsverlaufes bei Covid-19 und Long Covid einerseits und andererseits bei unerwnschten Nebenwirkungen nach den modRNA-Injektionen - auch im Vergleich zu anderen pathogenen Faktoren und Mechanismen - zu?
(2) Warum reagieren die Menschen so unterschiedlich auf eine Infektion mit SARS-CoV-19 und auch auf eine Covid-19-Impfung? Welche Rolle spielen hierbei die Sequenzdifferenzen und die Mehrfachexposition gegenber verschiedenen Spikecodierungen aus verschiedenen Impfungen und Infektionen?
(3) Was ist das Ausma§ und worin liegt die gesundheitliche Bedeutung der DNA- Verunreinigung in den modRNA-Covid-19-Impfstoffen? Und spielt diese Verunreinigung bei den berichteten Unterschieden in der Hufigkeit von Nebenwirkungen zwischen den verschiedenen Impfchargen eine Rolle?
(4) Wann erfolgen endlich Studien zur ãPharmakokinetikÒ (Verteilung, Stoffwechsel und Ausscheidung) dieser Impfstoffe? Welche Bedeutung hat die Pharmakokinetik fr die Behandlung von post acute covid syndrome oder post acute covid vaccinaton syndrome?
(5) Wie sehen mgliche Erklrungsmodelle fr einen Zusammenhang zwischen Krebs bzw. auch bestimmten Krebsarten und der Covid-19-Erkrankung bzw. -Impfung aus und welche empirische Evidenz gibt es fr solche Zusammenhnge?
(6) Wie hoch ist das Risiko einer Herzmuskel- oder Herzbeutelentzndung bei den angepassten Impfstoffen bzw. den aktuellen Virusvarianten?
(7) Wie kann eine routinetaugliche Methode zur Differenzierung zwischen Impf-Spike und Virus-Spike entwickelt werden, die Impfung und / oder Injektion als wahrscheinliche Ursache fr spikeassoziierte Erkrankungen auszumachen erlaubt?
Unsere Arbeit ist motiviert durch die Ð aus unserer Sicht mittlerweile hinreichend begrndete - Sorge um eine deutliche Unterschtzung der Nebenwirkungen der modRNA-Covid-19- Impfungen. Die Nebenwirkungen knnen auch erst nach lngerer Zeit, mglicherweise erst nach vielen Jahren auftreten Ð eine Annahme, fr die es mittlerweile einige wissenschaftliche Evidenz gibt.
Wir wollen eine Sensibilitt fr diese Probleme erzeugen, die fachliche Diskussion anregen und diese einer breiteren
ffentlichkeit zugnglich machen. Wir wnschen, dass wir mit unseren Einschtzungen falsch liegen. Aber nach drei Jahren intensiver Analyse verfgbarer Informationen und vieler Studien zu diesen Impfstoffen sehen wir immer gr§ere Risiken sowie offene Fragen, die dringend bearbeitet und beantwortet werden mssen. Deshalb fhlen wir uns Ð als kritische und eigenstndige Wissenschaftler Ð verantwortlich dafr, unser Wissen und unsere Fragen mit der
ffentlichkeit zu teilen. Wir danken allen, die diese Diskussion mit uns fhren.
Htte es einen solchen offenen Diskurs zu jedem Zeitpunkt der Corona-Episode in den Medien gegeben, wren uns wohl manche Fehler der letzten Jahre erspart geblieben.
Paul Cullen, Brigitte Knig, Jens Schwachtje, Henrieke Stahl, Henrik Ullrich
----------- ANHANG -------------
Zur Kritik an Robert Kennedy
Interview mit Tucker Carlson, 15.11.2021 (Transkript)
Ich habe Stichproben der Kritik an Robert Kennedy (z.B. imÊdeutschenÊundÊenglischenÊWikipedia) untersucht. Wegen der Sperrung von Kennedy's Instagram-Konto konnte ich die Gltigkeit der mich interessierenden, extremen Vorwrfe gegen ihn nicht verifizieren.
Vielleicht prfe ich die Haltbarkeit der kausalen Verbindung zwischen Impfung und Autismus als weitere Stichprobe. Problem: Dabei muss ich mich auf die Aussagen von Medizinern verlassen. Dass man sich bei Aussagen von Wissenschaftlern auf dnnem Eis bewegt, wissen wir aus eigener Erfahrung. Wir kennen die Scheu von Wissenschaftlern vor der bernahme von Verantwortung.
Gesellschaft fr Freiheitsrechte (GFF)
1. Gutachten Ausgangssperre
https://freiheitsrechte.org/home/wp-content/uploads/2021/04/GFF-Gutachten-Ausgangssperren.pdf
2. Zur Covid-19 hat sie eine bersichtlich gegliederte juristische Analyse im Internet:
https://freiheitsrechte.org/corona-und-grundrechte/
Das Papier "Corona und Grundrechte" wird -nach GFF-Aussage- fortlaufend auf den neuesten Stand gebracht. Diese Updates sind so alt, dass sie nach meiner Einschtzung noch nicht die neuerdings diskutierte allgemeine Impfpflicht im Anfang des kommenden Jahres (2022) behandeln.
UrteilÊdes Bundesverfassungsgerichts vom 30.11.2021 (im Cache)
|
"Wesentliche Erwgungen des Senats"
kann die verfassungsgerichtliche Kontrolle dabei von einer blo§en Evidenz- ber eine Vertretbarkeitskontrolle bis hin zu einer intensivierten inhaltlichen Kontrolle reichen. Daran gemessen verfolgte der Gesetzgeber mit den in ¤ 28b Abs. 1 Satz 1 Nr. 1 IfSG angeordneten Kontaktbeschrnkungen jeweils fr sich genommen und auch in ihrer Zusammenschau verfassungsrechtlich legitime Zwecke. Mit dem Vierten Gesetz zum Schutz der Bevlkerung bei einer epidemischen Lage von nationaler Tragweite bezweckte der Gesetzgeber ausweislich der Begrndung des Gesetzentwurfs, insbesondere Leben und Gesundheit zu schtzen.
Die Beurteilung des Gesetzgebers, es habe bei Verabschiedung des Gesetzes eine Gefahrenlage fr Leben und Gesundheit sowie die Gefahr der berlastung des Gesundheitssystems bestanden, beruhte auf tragfhigen tatschlichen Erkenntnissen. ... Belastbare Erkenntnisse, wonach nur geringe oder keine Gefahren fr Leben und Gesundheit durch eine Infektion oder nur geringe oder keine Gefahren auch durch berlastung des Gesundheitssystems vorlgen, waren jedoch nicht vorhanden.
4b. Die durch ¤ 28b Abs. 1 Satz 1 Nr. 1 IfSG angeordneten Beschrnkungen von Kontakten im privaten und im ffentlichen Raum waren im verfassungsrechtlichen Sinne geeignet, die Gesetzeszwecke zu erreichen. Dafr gengt bereits die Mglichkeit, durch die gesetzliche Regelung den Gesetzeszweck zu erreichen. Bei der Beurteilung der Eignung einer Regelung steht dem Gesetzgeber ein Spielraum zu, der sich auf die Einschtzung und Bewertung der tatschlichen Verhltnisse, auf die etwa erforderliche Prognose und auf die Wahl der Mittel bezieht, um die Ziele des Gesetzes zu erreichen. Dieser Spielraum reicht nicht stets gleich weit, sondern hngt einzelfallbezogen etwa von den Mglichkeiten ab, sich ein hinreichend sicheres Urteil zu bilden. Wiederum gilt zwar, dass bei schwerwiegenden Grundrechtseingriffen tatschliche Unsicherheiten grundstzlich nicht ohne Weiteres zulasten der Grundrechtstrger gehen drfen. Erfolgt wie hier der Eingriff aber zum Schutz gewichtiger verfassungsrechtlicher Gter und ist es dem Gesetzgeber angesichts der tatschlichen Unsicherheiten nur begrenzt mglich, sich ein hinreichend sicheres Bild zu machen, ist die verfassungsgerichtliche Prfung auf die Vertretbarkeit der gesetzgeberischen Eignungsprognose beschrnkt. Das schlie§t die Prfung ein, ob die gesetzgeberische Prognose hinreichend verlsslich ist.
|
Im Urteil wird nach meiner (JG) Einschtzung der schwachen Kopplung zwischen den Inzidenzen (Zahl der durch PCR diagnostizierten Neuinfektionen) und den Sterbefllen ungengend Rechnung getragen.Ê
Mit anderen Worten:Ê
(*) Der Schutz der durch COVD-19 lebensbedrohten Personen in Alten- und Pflegeheimen war trotz besseren Wissens unzureichend. Konkret: zu lange fehlten verlssliche Tests am Eingang dieser Einrichtungen, und dann wurden unzureichende Tests (nmlich Schnelltests anstelle von PCR-Tests) eingefhrt.
(*) Die Abwehr gravierender Schden htte also auch durch andere, weniger Grundrechts-einschrnkende Ma§nahmen als den vom Gesetzgeber beschlossenen Ma§nahmen (Bundesnotbremse) erfolgen knnen.Ê
Neil M. Ferguson (Epidemiologist)
He [Neil Ferguson] said that the new coronavirus could affect up to 60% of the UK's population, in the worst-case scenario,[53] and "suggest(ed) that the impact of the unfolding epidemic may be comparable to the major influenza pandemics of the twentieth century."[45][54][55] His team's publication in mid-March of the projections that the UK could face hundreds of thousands of deaths from COVID-19 without strict social distancing measures, gained widespread media attention.[56][57] In late March, he calculated that with "strict social distancing, testing and isolation of infected cases", deaths in the UK could fall to less than 20,000.[58]
Ferguson's research has raised questions by virologist Hendrik Streeck. Ferguson is the corresponding author for a paper titled "Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand", which describes itself as having "informed policymaking in the UK and other countries in recent weeks".[59] Streeck stated in reference to the paper "In the Ð really good Ð model studies by the Imperial College about the progress of the epidemic, the authors assume, for example, that 50 percent of households in which there is a case do not comply with the voluntary quarantine. Where does such an assumption come from? I think we should establish more facts."[60] The COVID-19 computer model which Ferguson authored (see CovidSim) was initially criticised as "unreliable" and "a buggy mess,"[61][62] but subsequent efforts to reproduce the results were successful.[63]
Josh Stirling
Josh Stirling: Dissecting Excess Death Data and How Insurance IndustryÕs Trillions Could Be Deployed to Help the Vaccine-Injured (im Cache)
ÒThe more doses on average you have in a region within the United States, the bigger increase in mortality that region has had in 2022 when compared to 2021,Ó said Josh Stirling, an insurance research analyst who has been dissecting alarming trends in life insurance, mortality and disability data over the past couple of years.
Looking at CDC data, Stirling ranked the number of doses administered across regions in the U.S. and compared that to the increase or decrease in mortality in 2022 compared to 2021. He said what he found was a clear regression line to the right. In other words, more doses correlated to greater increases in mortality.
He has also conducted extensive analysis of U.K. data which show greater mortality rates among the vaccinated than the unvaccinated in 2022, as well as German hospital data showing alarming trends in immune-related issues and female fertility.
According to Stirling, COVID-19 vaccine manufacturers have turned their backs on the vaccine-injured Ñand face essentially no financial consequences for doing so. But there is one multi-trillion industry that actually does have a big financial incentive to help the vaccine-injured, said Stirling. He is the founder of Insurance Collaboration to Save Lives.
ÒIf we were actually just screening for these people, the vast majority of these health issuesÑbefore they become catastrophicÑcould very easily be managed, not necessarily solved, but certainly managed with amazing medical advances and simple things like blood thinners, or changes in lifestyle,Ó he said.
ÒIf we can help at scale people understand their current health situation, then, absolutely, we can save a bunch of lives,Ó said Stirling.
Lab Leak - The True Origins of COVID-19
(alternate link: covid.gov)
After Action Review of the COVID-19 Pandemic: Lessons Learned and a Path Forward,
Dec. 4, 2024, Select Subcommittee on the Coronavirus Pandemic, Chairman Brad Wenstrup (im Cache)
Table of Contents
Preface
I. List of Key Names and Institutions ..................................................................................... i
II. List of Hearings and Meetings ........................................................................................... xi
III. List of Transcribed Interviews and Depositions .............................................................. xix
IV. On-the-Ground Oversight .............................................................................................. xxiii
The Origins of the Coronavirus Pandemic, Including but Not Limited to the Federal
GovernmentÕs Funding of Gain-of-Function Research
I. The Unknown Origins of COVID-19 ..................................................................................1
A. SARS-CoV-2, the Virus that Causes COVID-19, Likely Emerged Because of a
Laboratory or Research Related Accident .....................................................................1
B. ÒThe Proximal Origin of SARS-CoV-2Ó Was ÒPromptedÓ by Dr. Anthony Fauci to
ÒDisproveÓ the Lab Leak Theory ...................................................................................5
II. The Failures of EcoHealth Alliance, Inc. ...........................................................................58
A. EcoHealth Alliance, Inc. Facilitated Gain-of-Function Research at the Wuhan
Institute of Virology .....................................................................................................58
B. EcoHealth Alliance, Inc. Submitted its Year 5 Annual Progress Report Nearly Two
Years Late ....................................................................................................................68
C. EcoHealth Alliance, Inc. Failed to Timely Report a Dangerous Experiment to the U.S.
National Institutes of Health ........................................................................................78
D. EcoHealth Alliance, Inc. Failed to Provide the U.S. National Institutes of Health with
Research the U.S. Taxpayer Funded ............................................................................84
E. To Get a Grant Reinstated, EcoHealth Alliance, Inc. Misled the U.S. National
Institutes of Health Regarding the Physical Locations of U.S. Funded Samples ......102
F. The Defense Advanced Research Projects Agency Rejected EcoHealth Alliance,
Inc.Õs DEFUSE Proposal Because of a Lack of Gain-of-Function or Dual Use
Research of Concern Plan ..........................................................................................108
G. The Department of Justice Empaneled a Criminal Grand Jury to Investigate the
Origins of COVID-19 ................................................................................................ 119
III. The Failures of the National Institutes of Health and National Institute of Allergy and
Infectious Diseases ...........................................................................................................123
A. The U.S. National Institutes of Health and National Institute of Allergy and Infectious
Diseases Failed to Oversee EcoHealth Alliance, Inc. ................................................123
B. Dr. Anthony Fauci Played Semantics with the Definition of Gain-of-Function
Research .....................................................................................................................133
C. The U.S. National Institutes of Health and National Institute of Allergy and Infectious
Diseases Granted U.S. Taxpayer Funds to the Chinese PeopleÕs Liberation Army ...139
D. Senior National Institute of Allergy and Infectious Diseases Leadership Fostered an
Environment That Promoted Evading the Freedom of Information Act ...................140
E. A National Institute of Allergy and Infectious Diseases Freedom of Information Act
Official Apparently Aided Others in Efforts to Evade the Freedom of Information Act
....................................................................................................................................143
The Efficacy, Effectiveness, and Transparency of the Use of Taxpayer Funds and Relief
Programs to Address the Coronavirus Pandemic, Including Any Reports of Waste, Fraud,
or Abuse
I. The Paycheck Protection Program ...................................................................................146
F. The Paycheck Protection Program Was Rife with Fraudulent Claims Resulting in at
Least $64 Billion of TaxpayersÕ Dollars Lost to Fraudsters and Criminals ...............148
G. The U.S. Small Business Administration Did Not Properly Define Critical Internal
Roles and Responsibilities and Failed to Provide Actionable Guidance to External
Stakeholders to Manage Fraud Risk and Combat Paycheck Protection Program
Abuse. ........................................................................................................................149
II. Enhanced Unemployment Insurance ...............................................................................152
A. Fraudulent Unemployment Insurance Payments Total More Than $191 Billion ..... 153
B. States Failed to Improve Their Preparedness and Implement Data-Driven Oversight,
Leading to Increased Fraud Across All Pandemic-Related Unemployment Insurance
Programs ....................................................................................................................157
III. Economic Injury Disaster Loan Program ........................................................................159
A. The U.S. Small Business Administration Disaster Programs, Including COVID-19
Economic Injury Disaster Loans, Suffered Increased Vulnerability to Fraud and
Unnecessary Losses of at Least $200 Million. ..........................................................159
B. U.S. Small Business Administration Did Not Implement Proper Oversight Controls to
Prevent Fraudulent Economic Injury Disaster Loans ................................................161
IV. Transnational Fraud .........................................................................................................163
A. Lackluster Oversight Resulted in Transnational Criminal Organizations and
Fraudsters Stealing U.S. Taxpayer Money from Pandemic Relief Funds .................164
B. Domestic and International Fraudsters that Stole from Pandemic Relief Programs
were also Connected to Other Organized Crimes ......................................................165
V. Flaws in Pandemic Program Oversight ............................................................................166
A. Federal Agencies Overseeing Pandemic Relief Funds were Needlessly ÒSiloed OffÓ
from Each Other, Which Prevented Wholistic Tracking and Disbursing of Funds to
Prevent Fraud .............................................................................................................166
B. Federal Agencies Did Not Require and Failed to Validate Information Provided by
Applicants to Properly Verify Eligibility ...................................................................168
C. Federal and State Agencies Lacked Up-to-Date Financial Management Systems,
Failing to Meet Federally Mandated Modernization Requirements, Leading to
Billions of Dollars of American Taxpayer Money Improperly Paid or Stolen ..........169
The Implementation or Effectiveness of Any Federal Law or Regulation Applied, Enacted,
or Under Consideration to Address the Coronavirus Pandemic and Prepare for Future
Pandemics
I. Overreliance on the World Health Organization ..............................................................171
A. The World Health Organization Failed to Uphold Its Mission and Caved to Chinese
Communist Party Pressure .........................................................................................173
B. The Chinese Communist Party Violated Articles Six and Seven of the International
Health Regulations with No Repercussions ...............................................................180
C. The World Health OrganizationÕs Report Regarding the Origins of COVID-19 Was
Incomplete, Misleading, and Parroted Chinese Communist Party Propaganda ........182
D. The World Health OrganizationÕs Draft ÒPandemic TreatyÓ Does Not Solve the
OrganizationÕs Underlying Problems and May Affirmatively Harm the United States
....................................................................................................................................187
II. The Strategic National Stockpile Was Not Prepared to Address a Nationwide Viral
Pandemic ..........................................................................................................................189
A. Dating Back to the Obama Administration, the Strategic National Stockpile Was Not
Prepared for a National Public Health Emergency ....................................................190
B. States Must Mainatain Their Own Stockpile of Emergency Medical Supplies .........192
III. The United StatesÕ Unsecure Supply Chain Risks a Future Failed Pandemic Response .......
..........................................................................................................................................194
A. The United States Must Reduce Its Reliance on Other Countries, Particularly China,
for Pharmaceuticals and Medical Supplies ................................................................195
IV. The Six-Foot Social Distancing Requirement Was Not Supported by Science ...............198
A. There Was No Quantitative Scientific Support for Six Feet of Social Distancing ....198
V. Masks and Mask Mandates Were Ineffective at Controlling the Spread of COVID-19 ........
..........................................................................................................................................203
A. Public Health Officials Flip Flopping on the Efficacy and Use of Face Masks Without
Full Scientific Transparency Caused Mistrust in Public Health Establishments .......204
B. The Biden Administration Exceeded its Authority by Mandating Masks .................206
C. The U.S. Centers for Disease Control and Prevention Relied on Flawed Studies to
Support the Issuance of Mask Mandates ...................................................................207
D. Forcibly Masking Young Children, Ages Two and Older, Caused More Harm than
Good ...........................................................................................................................212
VI. Unscientific COVID-19 Lockdowns Caused More Harm Than Good ............................214
A. Enduring COVID-19 Lockdowns Unnecessarily Harmed the U.S. Economy ..........215
B. Enduring COVID-19 Lockdowns Unnecessarily Damaged AmericanÕs Mental Health
....................................................................................................................................215
C. Enduring COVID-19 Lockdowns Disrupted the Development of American Children
and Young Adults .......................................................................................................216
D. Enduring COVID-19 Lockdowns Unnecessarily had Severe Consequences for
AmericansÕ Physical Health .......................................................................................218
E. Despite Lacking Scientific Basis, Vaccine Passports Became a De Facto Lockdown
for Unvaccinated Americans ......................................................................................218
VII. Former New York Governor Andrew CuomoÕs March 25 Order Was Medical
Malpractice, and the New York Executive Chamber Attempted to Cover it Up .............221
A. The Cuomo AdministrationÕs March 25 Directive Was Antithetical to Known Science
....................................................................................................................................221
B. Contrary to Denials, Mr. Andrew Cuomo and the New York Executive Chamber Were
Directly Involved in the Decision that Led to the March 25 Directive .....................222
C. The New York Executive Chamber Reviewed and Approved the March 25 Directive
....................................................................................................................................225
D. The March 25 Directive Was Inconsistent with Applicable Federal Guidance
Regarding Hospital to Nursing Home Transfers and COVID-19 Related Infection
Control .......................................................................................................................230
E. The Cuomo Administration Terminated the March 25 Directive in Response to Public
Pressure, not a Change in Applicable Science ...........................................................234
F. Cuomo Administration Officials Believed Mr. Cuomo Directed the Issuance of the
ÒJuly 6 ReportÓ to Combat Criticism of the March 25 Directive ..............................237
G. The July 6 Report Was Not Independently Drafted by the New York State Department
of Health nor Peer Reviewed .....................................................................................238
H. Mr. Andrew Cuomo Reviewed and Edited the July 6 Report, and His Edits Were to
Make the ReportÕs Findings More Causal .................................................................243
I. Mr. Andrew Cuomo Was Involved in the ÒPeer ReviewÓ Process and Directed
Individuals Outside of the New York State Government to Review the July 6 Report
....................................................................................................................................252
J. The Executive Chamber Decided to Remove Out-of-Facility Death Data from the
July 6 Report ..............................................................................................................253
K. The New York Executive Chamber Made the Decision to Not Publicly Report Out-of-
Facility Deaths ...........................................................................................................259
L. Mr. Andrew Cuomo Acted in a Manner Consistent with an Attempt to Inappropriately
Influence the Testimony of a Witness and Obstruct the Select SubcommitteeÕs
Investigation ...............................................................................................................265
M. Mr. Andrew Cuomo Likely Gave False Statements to the Select Subcommittee in
Violation of 18 U.S.C. 1001 .......................................................................................274
VIII. While Testing for COVID-19 Was Flawed, Utilizing Public-Private Partnerships Resulted
in Readily Available and Accurate Tests ..........................................................................276
A. Career Scientists at the U.S. Centers for Disease Control and Prevention Undermined
Trust in Public Health by Overpromising and Underdelivering Early Testing Kits,
Including Knowingly Putting Tests with a High Failure Rate on the Market Without
Appropriate Disclosures .............................................................................................277
B. Public-Private Partnerships Were More Effective in Increasing Testing Production,
Distribution, and Capacity than Career Government Bureaucrats .............................280
IX. Rapidly Implemented Travel Restrictions Can Save Lives .............................................283
A. International Travel Restrictions Delayed the Spread of COVID-19 Early in the
Pandemic ....................................................................................................................283
B. But for the Chinese Communist Party Blatantly Downplaying and Lying Concerning
the Serious Threat Posed by COVID-19, Travel Restrictions Would Have Been
Imposed Earlier and Been More Effective .................................................................288
X. Government Perpetrated COVID-19 Misinformation .....................................................290
A. Public Health Officials Incorrectly Characterized the Lab-Leak Theory as a
ÒConspiracy TheoryÓ .................................................................................................290
B. The Biden Administration Employed Undemocratic and Likely Unconstitutional
Methods to Fight What It Deemed to Be Misinformation .........................................292
C. The Biden Administration and Many Public Health Officials Exaggerated the Power
of COVID-19 Vaccines ..............................................................................................296
D. The U.S. Food and Drug Administration and Other Public Health Officials Falsely
Implied that Ivermectin Was Only for Horses and Cows ..........................................300
The Development of Vaccines and Treatments, and the Development and Implementation
of Vaccination Policies for Federal Employees and Members of the Armed Forces
I. The Success of Operation Warp Speed ............................................................................301
A. Operation Warp Speed Was a Great Success and Helped Save Millions of Lives ....301
B. Then Presidential Candidate Joe Biden and Vice-Presidential Candidate Kamala
Harris May Have Contributed to Early Distrust of Operation Warp Speed and
COVID-19 Vaccines ..................................................................................................303
II. The Decision to Override the Advisory Committee on Immunization Practices .............305
A. The Biden Administration Arbitrarily and Without Scientific Support Announced
COVID-19 Vaccine Boosters Would be Available to All Americans .........................305
B. U.S. Centers for Disease Control and Prevention Director Rochelle Walensky
Overruled Expert Advisors in an Apparent Attempt to Satisfy President Joe BidenÕs
Arbitrary Vaccine Approval Goals .............................................................................309
III. The Review of PfizerÕs Biologics License Application .................................................. 311
A. The Biden Administration Sidelined Senior Scientists After They Expressed Concern
Regarding the Rapid Pace of Review of PfizerÕs Biologics Approval Application ...312
B. The Biden Administration Accelerated the Approval of PfizerÕs Biologics Approval
Application to Impose Vaccine Mandates ..................................................................322
C. U.S. Food and Drug Administration Officials Refused to Rebut Allegations the Biden
White House Was Involved in the Pfizer Biologics Approval Application ...............326
IV. Public Health Officials Disregarded Natural Immunity, Despite Its Proven Effectiveness
and Durability ..................................................................................................................331
A. Those Who Recovered From COVID-19 Were Conferred Infection Acquired
Immunity ....................................................................................................................331
B. Herd Immunity is a Real Concept and Occurrence supported by public health leaders
such as Dr. Fauci. There Was a Coordinated Effort from Public Health Officials to
Ignore Natural Immunity and Suppress Dissenting Opinions ...................................332
V. Vaccine Mandates Were Not Supported by Science and Caused More Harm than Good
..........................................................................................................................................336
A. COVID-19 Vaccine Mandates Caused Massive Collateral Damage and Were Very
Likely Counterproductive ..........................................................................................340
B. COVID-19 Vaccine Mandates Were Not Supported by Science ...............................346
C. COVID-19 Vaccine Mandates Hampered U.S. Military Readiness ..........................347
VI. The COVID-19 Vaccine, While Largely Safe and Effective, Had Adverse Events That
Must be Thoroughly Investigated ....................................................................................349
A. The Vaccine Adverse Event Reporting System is Insufficient and Not Transparent .......
....................................................................................................................................349
B. Existing Vaccine Safety Systems May Be Missing Important Safety Signals,
Especially Related to Neurological Conditions .........................................................353
C. The U.S. Centers for Disease Control and Prevention Created a new Surveillance
System Specifically for COVID-19 Vaccines but Has Not Been Fully Transparent in
Sharing the Data Collected in it .................................................................................355
VII. The U.S. GovernmentÕs Insufficient Systems for Compensating COVID-19 Vaccine
Injuries .............................................................................................................................357
A. The U.S. Government Is Failing to Efficiently, Fairly, and Transparently Adjudicate
Claims for COVID-19 Vaccine Injuries .....................................................................359
B. The Countermeasure Injury Compensation Program Failed to Handle a Mass-
Vaccination Program ..................................................................................................361
C. A Robust and Transparent Vaccine Injury Compensation Program Is Necessary for
Promoting Trust in Vaccines ......................................................................................363
D. Debating or Discussing Vaccine Injury Compensation is Not ÒAnti-Vax,Ó and
Implications Otherwise Are Counterproductive to Protecting Public Health ............364
VIII. The Erosion of the Doctor-Patient Relationship During the COVID-19 Pandemic ........366
A. Pandemic-Era Policy Often Disregarded or Outright Violated the Sanctity of the
Doctor-Patient Relationship .......................................................................................367
B. The Use of Off-Label Prescriptions Was Unjustly Demonized and Further Eroded the
Doctor-Patient Relationship .......................................................................................371
The Economic Impact of the Coronavirus Pandemic and Associated Government Response
on Individuals, Communities, Small Businesses, Health Care Providers, States, and Local
Government Entities
I. The COVID-19 PandemicÕs Impact on American Business ............................................376
C. Government Imposed Mandatory Lockdowns Were the Primary Cause of Temporary
and Permanent Business Closures, but Other Factors Contributed as Well ...............377
D. Business Closures Disproportionately Impacted Rural and Low-Income Areas and
Have Led to Long-Term Changes in These Areas .....................................................379
E. The Lack of Supply Chain Diversity Exacerbated Economic and Business Recovery
....................................................................................................................................383
II. The COVID-19 PandemicÕs Impact on American Workers .............................................387
E. Public Health OfficialsÕ Arbitrary and Overly Broad Mitigation Measures and
Aggressive Efforts to Squash Legitimate Scientific Debate Unnecessarily
Exacerbated Unemployment ......................................................................................389
F. Pandemic Unemployment Disproportionately Impacted Sectors with Lower Wage
Earners Compared to Higher Wage Earners, Such as Those in Professional Services,
and Lower Wage Earners Continue to Remain Unemployed at Higher Rates and Will
Likely Remain So Over the Next Decade ..................................................................393
III. The Federal ReserveÕs Efforts to Mitigate the Economic Impacts of the COVID-19
Pandemic ..........................................................................................................................397
A. The Federal ReserveÕs Aggressive, Early Actions Blunted Economic Damage of the
Pandemic but Contributed to Staggering Inflation in Late 2021 Through 2022 .......405
B. After Immediate Actions to Stabilize the Economy and Financial Markets, the Federal
Reserve Should Have Placed More Emphasis on Monitoring and Addressing Long-
Term Risks Associated with Prolonged Low Interest Rates and Increased Government
Debt and Ensuring that Policies Did Not Lead to Future Financial Instability .........407
C. The Federal Reserve Likely Exceeded Its Role and Responsibilities to Provide
Market Liquidity and Acting as a ÒLender of Last ResortÓ by Assuming the Role and
Responsibilities of the Department of the Treasury by Acting as a Spender to Prevent
Market Insolvency .....................................................................................................408
The Societal Impact of Decisions to Close Schools, How the Decisions Were Made and
Whether There is Evidence of Widespread Learning Loss or Other Negative Effects as a
Result of These Decisions
I. COVID-19 Pandemic-Era School Closures ..................................................................... 411
A. Long Term School Closures Were Not Supported by Available Science and Evidence
....................................................................................................................................412
II. The American Federation of TeachersÕ Influence ............................................................415
A. The American Federation of Teachers Is Not a Scientific or Medical Organization .......
....................................................................................................................................415
B. The American Federation of Teachers Did Not Support Reopening Schools and
Predicated Its Support for Reopening Schools on Non-Scientific Policies ...............416
C. The Biden AdministrationÕs U.S. Centers for Disease Control and Prevention Broke
Precedent and Shared a Draft Guidance with the American Federation of Teachers ......
....................................................................................................................................420
D. The American Federation of Teachers Advocated for Mitigation Measures that Were
Overly Broad and Not Scientific, including Closure Triggers, Delaying the U.S.
Centers for Disease Control and PreventionÕs Issuance of the Operational Strategy ......
....................................................................................................................................422
E. The U.S. Centers for Disease Control and Prevention Accepted American Federation
of Teachers Edits to the Operational Strategy ............................................................428
III. The Harmful Impacts from School Closures ...................................................................438
A. Pandemic-era School Closures Adversely Impacted Academic Performance that Will
Continue for Years .....................................................................................................438
B. School Closures Significantly Contributed to Increased Instances of Mental and
Behavioral Health Issues ............................................................................................440
C. School Closures Made an Already Alarming Trend in Declining Physical Health
Worse .........................................................................................................................441
Cooperation By the Executive Branch and Others with Congress, the Inspectors General,
the Government Accountability Office, and Others in Connection with Oversight of the
Preparedness for and Response to the Coronavirus Pandemic
I. The Biden AdministrationÕs U.S. Department of Health and Human Services Obstructed
the Select SubcommitteeÕs Investigation .........................................................................443
A. The Biden AdministrationÕs U.S. Department of Health and Human Services
Deliberately Obfuscated Evidence that Could Incriminate or Embarrass Senior Public
Health Officials ..........................................................................................................444
B. The Biden AdministrationÕs U.S. Department of Health and Human Services
Unreasonably and Possibly Illegally Limited Access to Key Witnesses ...................449
II. EcoHealth Alliance, Inc. and Dr. Peter Daszak Obstructed the Select SubcommitteeÕs
Investigation and Misled the Public .................................................................................456
A. EcoHealth Alliance, Inc. Obstructed a Congressional Investigation .........................456
B. EcoHealth Alliance, Inc. Doctored Documents It Released to the Public .................462
C. Dr. Peter Daszak Made False Statements to Congress in Violation of 18 U.S.C. 1001
and 18 U.SC. 1621 .....................................................................................................466
III. Dr. David Morens Likely Destroyed Evidence, Used Personal Email to Hide from
Accountability, and Acted Unbecoming of a Federal Employee .....................................467
A. Dr. David Morens Used Personal E-Mail Accounts to Avoid the Freedom of
Information Act and Accountability ...........................................................................467
B. Dr. David Morens Deleted Federal Records in Violation of 18 U.S.C. 2071 ............474
C. Dr. David Morens Shared Internal U.S. National Institutes of Health Information with
Dr. Peter Daszak and EcoHealth Alliance, Inc ..........................................................481
D. Dr. David Morens Used His Position as a Federal Employee and Assisted Dr. Peter
Daszak and EcoHealth Alliance, Inc Avoid Oversight ..............................................491
E. Dr. David MorensÕ Actions Violated U.S. National Institutes of Health Policy ........497
F. Dr. David Morens Acted in a Manner Unbecoming of a Federal Public Health Official
....................................................................................................................................501
G. Dr. David Morens Likely Provided False Statements to Congress in Violation of 18
U.S.C. 1001 and 18 U.S.C. 1621 ...............................................................................508
IV. New York Governor Kathy HochulÕs Administration Withheld Key Documents from the
Select Subcommittee Based on Claimed Privilege ..........................................................512
A. The Executive ChamberÕs Production Is Incomplete, Overly Redacted, and Withheld
Thousands of Responsive Records Without Apparent Legal Basis ...........................513
Version: 21.4.2025
Adresse dieser Seite
Home
Jochen Gruber