Translate paper using Google Translate or Deep L.
von Gerhard Memmert
zur Zeit der Veröffentlichung: Ordinarius, Institut für Energietechnik, Technische Universität Berlin
und
Mitglied im Projekt Sicherheitsstudien Entsorgung, PSE
von Joachim Gruber
Inhalt
G. Memmert berechnete die Radionuklidausbreitung innerhalb des Deckgebirges und aus ihm heraus und die daraus resultierende radiologische Belastung (Dosisraten) einer Bevölkerung, welche dort lebt oder ihr Trinkwasser und ihre Nahrungsmittel ausschließlich von dort bezieht. Er geht dabei von vier Annahmen aus, von denen die ersten drei schon zur Zeit des Abfassung des Berichts nicht mehr Stand der internationalen Forschung waren und die vierte 10 Jahre nach Memmerts Publikation von der Internationalen Strahlenschutzkommission als fragwürdig erklärt wurde:
- Die Radionuklide verteilen sich gleichmäßig in der Umwelt.
- Die gegenwärtig beobachtbare Verteilung des aus dem Salzstock austretenden Salzes ist über Jahrhundertausende unverändert geblieben.
- Der geochemische Einfluß des Gesteins und Bodens im Deckgebirge auf die Ausbreitung der Radionuklide kann mit einem einzigen Parameter (Kd) wiedergegeben werden.
- Die Radionuklidaufnahme in die Nahrungskette und den Menschen läßt sich für Jahrhundertausende mit den heute bekannten Modellen und Transferkoeffizienten beschreiben.
Latest version at: http://acamedia.info/sciences/J_G/references/memmert/deckgebirge.htm
Annahmen in der Publikation
Für die Berechnungen machte Gerhard Memmert folgende 4 einschränkende Annahmen:
- Es interessieren nur die Konzentrationen CS(i) (Bq/l) aller aus dem Endlager freigesetzten Radionuklide i im Grundwasser des Deckgebirges (einem Teil der Biosphäre). Aus den Konzentrationen werden durch Multiplikation mit Dosisfaktoren die Strahlenexpositionen der Menschen berechnet.
- Die Radionuklidkonzentrationen CS(i) werden mit verschiedenen Modellen berechnet, abhängig davon, ob die Radionuklide an einer eng begrenzten Stelle den Salzstock verlassen (1. Modell) oder nicht (2. Modell):
- Modell: Die Grundwasserbewegung wird mit einer Übertragungsfunktion berechnet. Die Parameter der Übertragungsfunktion werden in einem im Vergleich zur Radionuklidhalbwertszeit kleinen Zeitfenster gemessen.
- Modell: Im Grundwasser des Deckgebirges verteilen sich die aus dem Salzstock ausgetretenden Radionuklide wie das gelöste Salz. Diese Verteilung wird mit der einfachsten Differentialgleichung berechnet, d.h. der stationären Lösung einer linearen gewöhnlichen Differentialgleichung erster Ordnung mit konstanten Koeffizienten.
- Das geochemische Verhalten jedes Radionuklids RNi wird durch einen einzigen, pauschalen und konstanten Parameter Kdi charakterisiert, das Verhältnis von adsorbierter zu in Lösung befindlicher Konzentration des Radionuklids ("Kd-Konzept"). Er wird als konstant gewählt, weder seine räumliche noch seine zeitliche Entwicklung ist bekannt. Die Radionuklide folgen der Grundwasserbewegung v0, ihre Wanderungsgeschwindigkeit vRNi ist aber um den Faktor Ri (Retardierung) langsamer als die des Grundwassers (Ri = v0/vRNi). Werden adsorbierte und in Lösung befindliche Konzentration entsprechend definiert, ist Kd dimensionslos (und wird hier als kd bezeichnet: Ri = 1 + kdi).
- Die Strahlenbelastung (Dosisraten, Sv/a) durch vom Endlager kontaminiertes Grundwasser berechnet Memmert aus den Radionuklidkonzentrationen im Grundwasser (Bq/l) in zwei Schritten:
- Im ersten Schritt werden Expositionspfade (Details) festgelegt, auf denen die Radionuklide zum Menschen gelangen (Vorgehen der US Nuclear Regulatory Commission, USNRC, (im Cache): Gleichungen (1) - (5)). Es werden die Radionuklidaufnahmeraten (Bq/Jahr) entlang dieser Expositionspfade berechnet. Zentrale Pfadparameter sind Radionuklid-spezifische konstante Transferkoeffizienten, welche die Konzentrationsverhältnisse von einem Expositionspfadglied zum nächsten festlegen.
Beispielsweise ist der Transferkoeffizient
- für eine bestimmte Pflanze in der Nahrungskette gleich der Aktivität (Bq) des essbaren Teils dieser Pflanze pro kg (Naßgewicht) dieses Teils dividiert durch die Bodenaktivität (Bq) pro kg Trockengewicht des Bodens. Die Einheit dieses Boden-Pflanze-Transferkoeffizienten Biv ist folglich (Bq/kg Pflanze) / (Bq/kg Boden).
- analog dazu für im Wasser lebende Tiere auf der menschlichen Speisekarte gleich der Aktivität (Bq) des essbaren Teils dieser Seetiere pro kg dieses Teils dividiert durch die Kontamination des Wasser (Bq/Liter Wasser). Die Einheit dieses Wasser-Tier-Transferkoeffizienten Bip ist folglich (Bq/kg Tier) / (Bq/L Wasser).
- für ein auf Land gewachsenes tierisches Nahrungsmittel des Menschen gleich der Aktivität des tierisches Produkts (Bq) pro kg tierisches Produkt dividiert durch die Rate in Bq/Tag, mit der das Tier die Aktivität aufnimmt. Für diesen Boden-Pflanze-Tier-Transferkoeffizient ist die Einheit also (Bq/kg Tierprodukt) / (Bq/Tag). Bei vegetarischen Tieren wird die Aktivitätsaufnahmerate (Bq/Tag) wieder unter Verwendung des Transferkoeffizienten Biv Boden-Pflanze berechnet.
- Im zweiten Schritt wandelt man jede im Schritt 1 berechnete Radionuklidaufnahmerate (Bq/Jahr) durch Multiplikation mit einem Radionuklid-spezifischen Dosiskonversionsfaktor (Sv/Bq) in eine Dosisrate (Sv/Jahr) um. Werte dafür finden sich hier (im Cache) und hier (im Cache). Anschließend summiert man alle so berechneten Dosisraten zu einer Gesamtdosisrate auf.
Kritik an den Annahmen
Radionuklidwanderung (Annahmen 1 - 3)
Zu Annahme 1
Wegen der hohen und langlebigen Radiotoxizität des hochaktiven Abfalls sind schon kleinste Radionuklidmengen gefährlich, und daher darf man
-
nicht annehmen, daß sich die aus dem Salzstock austretenden Radionuklidinventare gleichmäßig verteilen werden, wie es das Salz anscheinend tut (mehr unter Kritik zu Annahme 3).
- die Analyse nicht auf das Deckgebirge beschränken, sondern muß den Weg der aus dem Deckgebirge in die Biosphäre freigesetzten Radionuklide über Jahrhunderttausende verfolgen. Wenn in dem betroffenen Gebiet weiterhin wie heute Lebensmittel angebaut werden, wandern die Radionuklide mit den Nahrungsmitteln. Dabei können Millionen von Menschen beeinträchtigt werden.
Zu Annahme 2
Annahme 2 geht davon aus, daß sich die heutige Salzverteilung (2. Modell in Annahme 2) oder die heutigen Grundwasserbewegungen (1. Modell in Annahme 2) während der notwendigen Isolationszeit des radioaktiven Abfalls nicht wesentlich ändern werden, d.h. die geologisch-geochemischen Verhältnisse so bleiben, wie wir sie heute antreffen. Ortoleva hat diese Annahme in Frage gestellt.
Zu Annahme 3
Kd eines Radionuklids ist nicht konstant, sondern variiert mit den geochemischen Bedingungen (Beispiel). Annahme 3 ist daher unvereinbar mit den Empfehlungen zur Benutzung des Kd (im Cache).
Wenn man ein konstantes Kd annimmt, schließt man die meisten der heute bekannten geochemischen Prozesse aus. Das Konzept konstanter Kd (chapter 2.3.1 Constant Partition Coefficient (Kd) Model, Seite 2.16 in "UNDERSTANDING VARIATION IN PARTITION COEFFICIENT, Kd, VALUES", Volume I: The Kd Model, Methods of Measurement, and Application of Chemical Reaction Codes, United States Environmental Protection Agency, Office of Air and Radiation, EPA 402-R-99-004A, August 1999 (im Cache)
- kann die räumlichen und zeitlichen Muster der Elemente in der Natur nur in wenigen Spezialfällen erklären. In der Natur entstehen meist ungleichmäßige Verteilungen, z.B. durch Selbstorganisation, und ebenso können sich die Radionuklide in der Biospäre zu Ansammlungen ("sekundären Endlagern") zusammenfinden in den Jahrhunderten und Jahrtausenden, nachdem sie das von Menschen gebaute (primäre) Endlager verlassen haben und noch nicht zerfallen sind.
- führt auch zu falschen wandernden Radionuklidmengen, d.h. nicht nur die Radionuklidverteilungen, sondern auch deren Inventare in der Biosphäre entwickeln sich grundsätzlich anders, als es das Kd-Konzept vorhersagt.
Dessen ist sich Memmert offensichtlich nicht bewußt: Im Literaturverzeichnis zitiert er keine Arbeiten zur Geochemie der Ausbreitung von Schadstoffen, obwohl Darstellungen wesentlicher Problemfelder im Jahr 1996 schon in Monographien vorlagen. Beispiele:
-Interessant in diesem Zusammenhang: Die aus dem Chernobyl-Reaktor entlassenen Radionuklide haben sich in der globalen Atmosphäre ungleichmäßig verteilt. Figure 1 in Lange, R., Dickerson, M.H. & Gudiksen, P.H., Dose Estimates from the the Chernobyl Accident, Nucl. Techn. 82: 311-322, 1987. UCRL-96934 Preprint, CONF - 871101 -- 78 (in cache)-
Radiologische Belastung (Annahme 4)
Schritt 1:
Die Konzentrationsverläufe entlang der Expositionspfade sind durch die Transferkoeffizienten gegeben. Man weiß, daß z.B. Schwermetalle sich in der Umwelt anreichern (Beispiel: Radiocaesium-belastete Pilze). Die Abläufe dabei gleichen der Anreicherung in der Geosphäre. Je länger ein Expositionspfad ist, desto stärker kann die Anreicherung werden (Beispiel: Bioakkumulation in Fischen, beschrieben im Transferkoeffizienten Bip). Die langlebigen Radionuklide können Teil der Biosphäre werden, indem sie sich in dem an den Boden gekoppelten Kreislauf Boden-Pflanze-Tier-Klärschlamm-Boden anreichern. Dann würden (bisher nicht berechenbare) Teile der aus dem Endlager ausgetretenden Radionuklidinventare in die Biosphäre verlagert.
Die Boden-Pflanze-Transferkoeffizienten beispielsweise variieren abhängig von Bodenchemie und -physik um mehrere Größenordnungen (z.B. Chapter "2.3.4.3. Radionuclide transfer from soil to crops" auf Seiten 52-55 von: Report of the Chernobyl Forum Expert Group 'Environment', "Environmental Consequences of the Chernobyl Accident and Their Remedediation: Twenty Years of Experience", IAEA, 2006 (im Cache)). Für endlagerrelevante Zeiträume ist die Charakterisiserung eines Expositionspfads durch konstante Transferkoeffizienten daher ähnlich irreführend wie die der Wanderung von Schadstoffen in der Geosphäre durch ein konstantes Kd.
Die für die Variation der Transferkoeffizienten verantwortlichen Umweltparameter (z.B. die chemischen und physikalischen Eigenschaften des Bodens) verändern sich über die Jahrhunderttausende in bisher unbekanntem Maße. Daher sind die in diesem Schritt berechneten Radioaktivitätsaufnahmen (Bq/Jahr) mit einem unbekannten Fehler behaftet.
Schritt 2:
Die International Commission on Radiological Protection (ICRP) findet die Verwendung von Dosiskonversionsfaktoren zur Berechnung der radiologischen Belastung über Jahrhundert(tausend)e fragwürdig:
"(e) In the distant future the geological disposal facility might give rise to some releases to the accessible environment and the "safety case" has to demonstrate that such releases, should they occur, are compatible with regulation and radiological protection criteria. In application of the optimisation principle, the reference radiological impact criterion for the design of a waste disposal facility recommended by ICRP is an annual dose constraint for the population of 0.3 mSv in a year [ICRP 103], without any weighting of doses in the far future. For less likely events resulting in potential exposures, the Commission continues to recommend a risk constraint for the population of 1 10-5 per year. However, ICRP Publication 103 also warns that, human habits and characteristics is such that effective dose looses its direct connection to health detriment after the time span of a few generations. At the same time, in the distant future, the geosphere and the engineered system and, even more, the biosphere will evolve in a less predictable way. The scientific basis for dose and risk assessments at very long times into the future then becomes questionable and the strict application of numerical criteria may be inappropriate. Hence, the annual dose constraint of 0.3 mSv in a year is to be used for the sake of comparison of options rather than as means of assessing health detriment." Quelle: Executive Summary, "Radiological Protection in Geological Disposal of Long-Lived Solid Radioactive Waste", ICRP PUBLICATION XXX, Annals of the ICRP, ICRP ref 4838-8963-9177, July 21, 2011 (DRAFT REPORT FOR FOR CONSULTATION) (im Cache, 6.10.2011).
Darüberhinaus ignoriert der Dosiskonversionsfaktor strahlungsinduzierte Störungen des allgemeinen Gesundheitszustands der Bevölkerung und in deren Folge der sozialen Verhältnisse. (Soziale Folgen der Strahlenschädigung durch den Unfall von Chernobyl).
Zusammenfassung
Seine Ergenisse faßt Memmert in einer graphischen Darstellung zusammen:
|
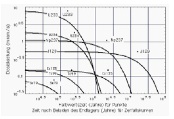
zum Vergrößern auf Bild klicken
|
Abbildung: Dosisraten für Radionuklide (mit Halbwertszeit T > 65000 Jahre und Dosisrate > 0.1 mrem/a) in der Biosphäre nach vollständiger Radionuklidfreisetzung aus dem Endlager. 1 mrem = 0.01 mSv.
Punkte: y-Koordinate: Dosisrate bei Freisetzung innerhalb eines Zeitraums nach Beladen des Endlagers. Annahme: Dieser Zeitraum ist um wenigstens eine Größenordnung kürzer ist als die Halbwertszeit des Radionuklids, x-Koordinate: Halbwertszeit des Radionuklids.
Kurven: Dosisraten als Funktion der Zeit nach Beladen des Endlagers. Die Dosisraten wurden "ohne Transportkorrektur" berechnet, d.h. die Zeit für Wanderung der Radionuklide durch das Deckgebirge in die Biosphäre wurde sicherheitshalber als wesentlich kürzer als deren Halbwertszeit angesetzt, also der Zerfall der Radionuklide auf der Wanderung in die Biosphäre blieb unberücksichtigt.
Quelle der Daten: G. Memmert.
(Anmerkung: Das Radionuklidinventar im angenommenen Endlager ist um etwa den Faktor 300 höher als das im Reaktor von Chernobyl.)
Am 2. 8.1982 schreibt Gerhard Memmert: "Für die Problemnuklide Tc, J, Np erscheint die Barrierewirkung des Deckgebirges zur Zeit nicht ausreichend." Weiterhin führt er aus, daß der Standort Gorleben nur "einer der zweitbesten" sein dürfte. (Quelle: Bericht zur Frage der politischen Einflussnahme auf den Zwischenbericht der PTB zur weiteren Erkundung des Standortes Gorleben (1983), im Cache)
|
Gerhard Memmert bewertet seine Analyse mit folgenden Worten:
"Das Deckgebirge über einem Salzstock ist bei einer Dicke von etwa 250 m bis 300 m eine sehr effektive Barriere für Schadstoffe, die möglicherweise aus einer Deponie im Salzstock austreten können. Die Wirksamkeit dieser Barriere läßt sich ohne aufwendige und detaillierte Rechnungen ermitteln. Benötigt werden dazu lediglich Daten, welche die Verteilung der im Deckgebirge gelösten Mineralsalze beschreiben, sowie Grundwassermengen und Salzfrachten, die aus dem Deckgebirge in die Vorfluter austreten. Alle diese Daten sind im Beispiel des Salzstocks Gorleben bekannt."
...
(Es folgt eine zusammenfassende Darstellung der verwendeten Modelle und Ergebnisse. Die Zusammenfassung endet mit folgendem Satz.)
...
"Aus allem wird deutlich, wie außerordentlich groß das Sicherheitspotential des Endlagers allein durch die Struktur des Deckgebirges einzuschätzen ist."
Die Publikation ist Teil der mit öffentlichen Mitteln geförderten Langzeitsicherheitsforschung des deutschen nuklearen Establishments. Auf sie stützt sich die deutsche Regierung mit ihrer Aussage, die gegenwärtige Generation sei verpflichtet, noch zu ihren Lebzeiten den hochradioaktiven Abfall endzulagern. Wegen der oben beschriebenen gravierenden Beschränkungen der verwendeten Modelle und Parameter erfüllt die von Gerhard Memmert vorgestellte Forschung nicht die in diesem Rahmen notwendigen Qualitätsanforderungen. Diese Kritik konnte man schon zur Zeit ihrer Veröffentlichung auf Grund der damals vorliegenden Literatur üben.
Nach meiner Erfahrung
- hat sich die Qualität der nuklearen Langzeitsicherheitsforschung seither nicht verbessert (einige Gründe dafür),
- beweist die von Gerhard Memmert vorgestellte Forschung, daß die Organisation dieses Wissenschaftszweigs grundlegend reformiert werden muß, damit die Wissenschaftler ihrer Verantwortung gegenüber der Gesellschaft gerecht werden.
Version: 22 October 2017>
Adresse dieser Seite
Home
Joachim Gruber
