This paper is an updated version of J. Gruber, "Natural Geochemical Isolation of Neutron-Activated Waste:Scenarios and Equilibrium Models", Nuclear And Chemical Waste Management Vol.8, pp. 13-32, 1988
Natural Geochemical Isolation of Neutron-Activated Waste: Scenarios and
Equilibrium Models
Joachim Gruber
Address at the time this paper was finished (1985):
Department of Civil Engineering and School of Earth Sciences
Stanford University, Stanford, CA 94305, USA
Address as of March 1988:
Department of Soil & Environmental Sciences, UCR, Riverside, CA 92521, USA
ABSTRACT
A coupled geochemical/geohydraulic model is used to discuss and interpret possible mechanisms for contaminant transport and accumulation in inorganic environments.
Scenarios are constructed incorporating computed system behavior. A comparison of potential contaminant concentrations with acceptable ones allows us to quantify the degree of geochemical isolation of the contaminant which a chosen environment provides. Long lived radioactive waste generated in the thermal neutron flux of a light water reactor is assessed using the proposed methodology and a very conservative scenario.
- Beryllium, lead, molybdenum, selenium, tin and zirconium activated in the bulk of the reactor decommissioning waste (the bioshield) might be sufficiently isolated by the chemistry in common soils.
- The concentration of nickel in oxidizing inorganic noncomplexing drinking water has an upper limit given by the precipitation of nickel minerals. Environments above pH = 7 have an effective geochemical barrier for nickel activated anywhere in the reactor except the high neutron flux region.
INTRODUCTION
Natural concentrations of trace elements are the result of an interplay of physical (advection, dispersion, etc.) and chemical processes (weathering, etc.). Although large variations of the parameters determining the processes of both classes have been observed, typical natural concentrations in sedimentary low temperature environments of a number of elements lie in a comparatively small range.
This suggests the notion of typical environments. To the degree that physical and chemical processes are independent from one another, a typical natural geochemical environment can be defined. This, in turn, can be characterized by typical values of such environmental parameters as pH, Eh and the concentrations of other cations or anions in the system. Because of their radiotoxicity, radioactive waste elements will always play the role of trace elements in biosphere environments. Waste elements are therefore describable as being subject to chemical processes of any environment (e.g., the typical one) without themselves being able to change or considerably modify it.
Quantitative geochemistry has developed to such an extent that now its methods and models enter into the field of waste impact assessments. Nevertheless, in low level radioactive waste assessments, traditionally only a small subset of the many possible processes have been considered. For example, the major environmental characteristics of a contaminant plume in a porous medium are the breakthrough concentration and the migration velocity.
- The former, the breakthrough concentration, is assumed to be given by the balance between mobilization of the waste element from the waste environment (trench) and dilution by the percolating water intruding into the trench (1);
- The latter, the migration velocity, is assumed to be a superposition of retarded velocities along individual flow paths, assuming that those velocities are either all identical or have a stochastic distribution, (i.e. no deterministic spatial correlation among each other or along the flow path).
Coupled geochemical/geohydraulic transport models do not always make these assumptions. The central part of this paper, therefore, will be to construct a more general set of typical environments and their temporal changes (so called scenarios) based on such transport models. This will lead to scenario-dependent radionuclide concentrations and radionuclide intakes by man that are independent of the performance of engineered barriers enclosing the waste. These concentrations are given by the same natural geochemical processes that have led to the narrow concentration ranges mentioned above and to the isolation of life from natural toxic substances in the biosphere.
These concentrations will be used for the three objectives of this paper, an estimate of
- the ability of the common soil to contain elements of the broad spectrum of long lived neutron activation products (i.e. sufficiently keep them out of the biosphere),
- the ability of a variety of soils and rock environments to isolate nickel, which is chosen as an example for a major activation product, and
- the time after shut-down of the reactor during which activated nickel has to be kept separate from those biosphere environments the geochemistry of which provides insufficient natural containment.
2. BACKGROUND
Three types of models are combined to assess the impact of radioactive waste.
- The first, an environmental model together with scenarios, provides values of elemental concentrations Cw or Cs in the pore water or on the solid phase of the porous medium.
- The second, an activation model (2,3) allows calculation of the specific activity of those elements which are generated upon exposure to neutrons in a reactor.
- The third, a radiological model, is tailored to provide the link between the other two models.
The input to the radiological model consists of a choice of
- a radionuclide intake pathway,
- a metabolism and
- an arbitrarily fixed reference level for the radiation exposure.
The model converts the specific activity into a reference concentration Cp of the waste element at the biota access location (i.e. one which leads to the assumed exposure level). This concentration is then compared with the environmental concentration Cw or Cs provided by the environmental model. If the reference exposure level is the maximum permissible one, Cw < Cp means that the geochemistry of the environment is able to isolate the waste. The assumptions of the radiological model as used in this paper are:
- intake pathway: drinking water
- metabolism of Reference Man (4)
- radiation exposure limits: 10% of the ones recommended by the International Commission on Radiological Protection (ICRP) for occupationally exposed workers (5).
When a single radionuclide dominates the radiation exposure, the reference concentration may be chosen as:
Cp(t) = 0.1ALl/(S(t) m) .................... [1]
where 0.1 is the ratio of the exposure of a member of the most exposed group of the population and the exposure of occupationally exposed workers (for meaning of other symbols see Notation section below).
S(t) is the specific activity of the element at time t after reactor shut-down, i.e., the activity of the element per weight of the element consisting of stable and radioactive isotopes). The time dependence is given by the radioactive decay of the radionuclide:
S(t) = S(t=O) exp(-t ln2/T)
where T is the half life of the radionuclide.
For short, the radiation exposure limit stated in 3. will be arbitrarily called ''permissible." If, on the basis of this radiological model, the calculated radiation exposure in an environment is below the ''permissible'' limit, the abbreviated description will be: The environment is able to "sufficiently isolate'' the waste element. Likewise, Cp will sometimes be called "permissible'' or reference concentration, and if the concentration in the environment is below the "permissible" one, due to geochemical processes, the waste is said to be "contained" or "locked up'' in a "geochemical cage".
A geohydraulic model coupled with an equilibrium speciation model (see paragraph 2.A) is the environmental model mentioned above. It is used as a basis for estimating potential concentrations of the radioactive elements in the affected environment. Contaminant transport scenarios (see 2.B) are used to enter information into these estimates which is presently not contained in or not obtainable from models.
2.A . Equilibrium Speciation Models: Calculation of Distribution Coefficient
Once a pollutant M has migrated through the barriers of the repository, its fate is determined by groundwater movement and geochemical interactions in the system. Transport of the pollutant can therefore be modeled by coupling the equations describing those two processes.
Due to geochemical interactions the pollutant element M is partitioned in the system, which means that it is incorporated into the following chemical species:
- free ion
- soluble complexes
- (insoluble) precipitates
- sorbed on soil particles.
Various approximations are nevessary to calculate the partitioning of M. A common one is the assumption of chemical equilibrium which is adopted here.
If M is present at trace concentrations, the system decouples into two subsystems: the environment with its interactions undisturbed by trace M (the ''background''), and M. The background ion concentrations have nonlinear interrelations among each other, which have to be resolved numerically. In contrast, the concentrations of the species of M are proportional to the concentration of M, PjT, and can be expressed by simple ''side reactions":
[Pj]/PjT = 1/(1 + Σk σk)................... [2]
[Ql]/PjT = (σl/(l + Σk σk)................... [3]
Notation
The side reaction coefficient σl describes the reactions between the pollutant and the background. It is simply a product of the reaction equilibrium constant and free background ion concentrations. PjT, the ''total'' concentration of M, is the sum of the concentrations of the free M and the M containing complexes.
Traditionally, sorption has been characterized by the distribution coefficient Kd, which is the ratio between the concentration Cs of the sorbed species and the sum Cw of the concentrations of the soluble species (1. and 2., see above).
Cs = Kd Cw................... [4]
Notation
Over the years the Triple Layer Model (7) has been developed, a common theoretical model for some of the major sorption processes, the so called "adsorption" processes. In this model, side reactions k leading to adsorption of components are treated mathematically identically to side reactions l leading to complex formation:
Kd = Kd ( {[Pn]} ) = const Σkσk /( l + Σlσl)................... [5]
Notation
where the sum in the numerator extends only over the adsorbed species k, whereas the one in the denominator extends over only soluble species l. const is unity if Cs and Cw are measured in the same units; it is the dimensional factor ρ/n (which is the weight of soil present in a system volume of one liter) if, as usual, Cw is measured in gram per liter of water and Cs in gram per kg of soil. {[Pn]} is the set of environmental parameters having an effect on or entering into the explicit expressions of the side reaction coefficients in Eq. 5.
TABLE 1
Parameters Determining Equilibrium Partitioning of
Trace Contaminants
- Physical/Mineralogical Background Parameters: Adsorbent
- composition and mineralogy of soil/rock and of its alteration (wheathering) products,
- specific surface area of adsorbing phases,
- cation or anion exchange capacity,
- electrostatic properties of surface/water interface.
- Chemical Background Parameters: Adsorbent
- adsorption reactions,
- reaction equilibrium constants for major and contaminant ions.
- Physical and Chemical Background Parameters: Pore Water
- concentrations of major ions and trace organic complexing agents,
- electrochemical potential,
- solubility products.
- complex formation constants.
- Nuclide Properties
- adsorption reactions and equilibrium constants,
- complex formation reactions and constants.
Because of the complexity of the side reactions leading to adsorption of M, Kd is not a constant. It is not independent from Cw and depends on the set of parameters describing the state of the background.
Of the many computer codes (8) developed to calculate the free background ion concentrations some have grown into families of codes (9). Because adsorption is treated as complexation, all equilibrium speciation codes can calculate Kd. A major group of adsorbents (e.g., oxides) develop electrical charge on their surfaces which changes with background ion concentration. The codes of the REDEQL family are able to calculate the change of surface charge and thus adsorption properties of oxides with background ion concentration. The computations in this paper were made with the code MINEQL-SGMA (10), an enlarged version of MINEQL (11) of the REDEQL family. It uses the Triple Layer Model (12) to calculate adsorption on surfaces with variable surface charge.
Figure 1 displays a typical example of computed Kd variations with background ion concentrations. It shows adsorption of the Ni2+ cation on goethite (a common iron oxide in soils). The proton, calcium, sodium, carbonate, chloride and sulfate (background ions, also called major ions) are assumed to adsorb in addition to the pollutant (nickel). Reactions and data are taken from references (13, 24) (see Appendix A).
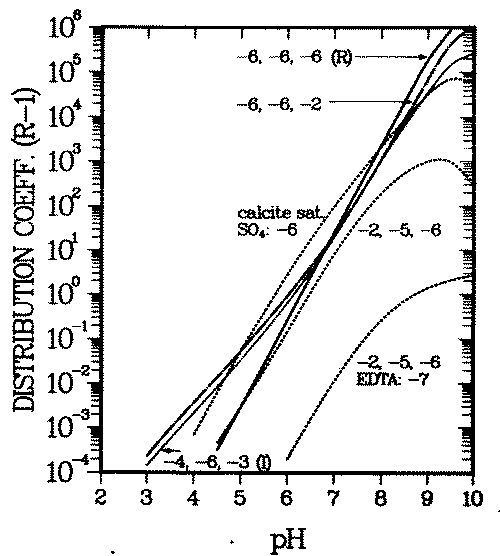
FIGURE 1:Variation of the distribution coefficient (see Eq. 6 for definition) of nickel with solution composition. The numbers at the curves give the logarithms of the total calcium, carbonate and sulfate concentrations, respectively, if not denoted otherwise. "Calcite sat" means that the water is saturated with respect to calcite, the total calcium and carbonate concentrations being equal. The other parameters used and the reactions considered in the calculations are given in Appendix A.
The figure shows the influence of the following three basic effects of major ions on the adsorption of a cationic contaminant when adsorption varies with surface charge:
- increased competition for adsorption sites reduces Kd (e.g., decrease of Kd with increasing proton or calcium concentration),
- increased (soluble) complexation of the pollutant reduces Kd, see decrease of Kd even when a small concentration of EDTA is introduved,
- increased electrostatic repulsion from or reduced electrostatic attraction to the surfave reduces Kd. Adsorbed calcium cations repel the contaminant from the surface, adsorbed carbonate or sulfate anions attract it onto the surface. Figure 1 shows the latter below pH = 7.5, where soluble contaminant complex formation and competition for adsorption sites are negligible in the chosen example.
A further effect known to influence the solid/solution partitioning, Kd, is ion exchange in the diffuse layer. Contrary to the two layers in which the above mentioned surfave complexation processes bind ions to the surface, in this third layer considered in the Triple Layer Model, the ion-surface bond has no chemical contribution. The ions are assumed to be bound exclusively by electrostatic forces. The influence of ion exchange on contaminant transport is not qualitatively different from processes 1 - 3, and will here be simulated by those processes .
Because adsorption onto goethite surfaces can dominate trace element concentrations in soils (25), background dependent variations of Kd are probably at least one order of magnitude. Such variations have been observed for a wide range of elements (26). It will be shown in the next section that such Kd variations can lead to contaminant accumulations which migrate with anomalously large velocity .
2.B Transport Models: Calculations of Roll Fronts
The hydraulic equations describe the motion of soluble species. The contaminant transport equation is a simple time transform of the equation describing the movement of the carrier (water), if Kd is approximated by a constant, (i.e., is assumed to be independent from time and changes of the background). The transformation is
t' = t (1 + ρ/n Kd) = t R ................... [6]
Notation
where t' is the time variable in the contaminant transport equation, t is the time variable in the water transport equation.
For example, the velocity of the contaminant v' is related to the one of the carrier, v, by
v' = v/R.................... [7]
Notation
The migration of the plume can become more complizated than that when the background environment (and thus Kd) is allowed to change with time.
One new phenomenon in such an environment is roll front formation, an effect that has long been known in the geology of sedimentary ore formation or in ion chromatography (there known under the name ''deposition front"): Water differing in its chemical composition from that in the deposit (or in our case the contaminant plume) enters. If the response of the system is to release precipitated or adsorbed ions into solution, these ions will be transported in the solution phase and re-deposited in parts of the deposit not yet affected by the intruding water, (i.e. ahead of the intruding remobilization front). This process is sometimes called formation of a secondary deposit.
Roll fronts are known to be capable of migrating fast and over large distances (27). They have been observed in uranium deposits (27), in waste plumes (28, 29, 30) and in natural uncontaminated soils (31).
The basic process forming a roll front is most easily described in the following simple example in which Eq. 6 (i.e. the conventional retardation factor approach), can still be used to a limited extent.
The initial deposit of the contaminant is characterized by a spatially uniform distribution coefficient, Kd0,M . A perturbation is introduced by having water intrude from outside and change (e.g., increase) the concentration of a major ion (''remobilizing" ion), such as calcium, in the pore water of the deposit. This causes the distribution coefficient of M to decrease from Kd0, M to Kdr, M. The model computations (Figure 1) show that a decrease by a factor of ten is possible if the calcium concentration increases to 10-2 M. On the other hand also, calcium is partitioned between solid (oxide surfaces) and solution in the plume environment, its distribution coefficient being Kdf . The intruding front of elevated calcium concentration will migrate with a corresponding retardation. Qualitatively, Figure 1 is typical also for calcium, the actual curves for calcium will only be shifted parallel to the ones in Figure 1.
If Kdf is intermediate between Kd0, M and Kdr, M , an observer located on the calcium front will see contaminant migrating toward him regardless whether s/he looks in the direction of the movement of the front (''forward'' or downstream) or against it ("backward'' or upstream). Contaminant will therefore accumulate at the front while the front sweeps over the deposit (56). In the special case when the front is not retarded (Kdf = 0), no contaminant can enter the front from the upstream direction. Only then the entire accumulated inventory will be soluble, whereas in the general case (Kdr, M < Kdf < Kd0, M) that inventory will be partly adsorbed and partly in solution. The soluble fraction of the accumulated inventory will rapidly increase with decreasing Kdf when the system crosses the desorption threshold of the remobilizing cation, Kdf = 1 (see Figure 1 and Appendix A for details of the pertinent parameters and environmental concentrations) .
The discussion of some aspects of solution dependent distribution coefficients and their influence on contaminant transport will be finished here by giving a quantitative picture of how a roll front can be generated in a deposit adsorbed onto goethite. The response of a nickel deposit is computed for the case of intruding water with a high sulfate concentration. The results for different time steps are displayed in Figure 2.
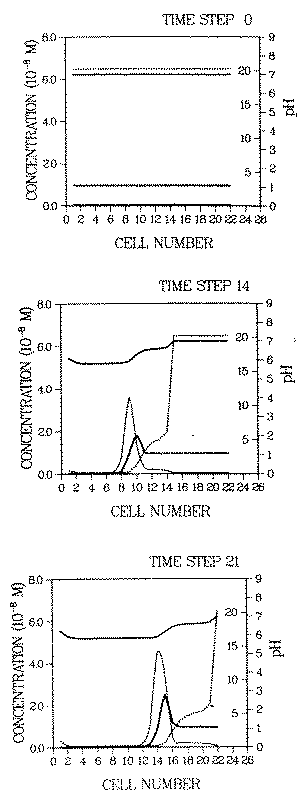
FIGURE 2:Development of a pH (top solid line), Kd(top line, dotted) and contaminant roll front, the latter consisting of a soluble (thin line) and adsorbed part (heavy line). The ordinate on the right inner margin gives the values of Kd. The environment is approximated by an array of cells. The immobilization/remobilization process is ad/desorption on/from goethite surfaces. Details of the calculations are given in Appendix A. The fronts are generated by intrusion of water which lowers the distribution coefficient of the contaminant (see Figure 1) as well as that of protons (i.e. it desorbs those ions). The contaminant distribution coefficient in the intruding water is given by curve R and the one in the onginal plume pore environment (prior to the intrusion of the new water) by curve 1 in Figure 1
The environment is approximated by an array of cells ("chromatographic column"), through which the water flows from left to right. The longitudinal dimension of each cell is chosen so that within each cell complete mixing of the pore water (due to hydrodynamic dispersion) and thermodynamic equiIibrium can be assumed. The increment between time i and i + 1 is the time necessary for the pore water in cell k to replace the one in cell k+1 (i and k are arbitrary numbers).
Initially the spatial distribution of the contaminant is uniform. The concentration of the adsorbed waste element is assumed to be l0-8 M, consistently with the assumption of M being a trace. At the pH of the plume environment (pH = 7) the soluble contaminant concentration is 4.7 10-10 . The adsorbed concentration is represented by a heavy line, the soluble concentration by a light line. The top curve gives the pH, the dotted curve gives Kd.
The initial total (i.e. adsorbed and soluble) concentrations in the plume environment are as follows:
calcium ................... I0-4 M
sodium ................... l0-2 M
carbonate ................... 10-6 M
chloride ................... l0-2 M
sulfate ................... 10-3 M
pH ................... 7.0
The pH dependence of the waste element distribution coefficient for this environment is given by curve (I) in Figure 1. The corresponding concentrations in the intruding water are all 10-6 M, and its pH is the same as in the plume (pH = 7). The corresponding waste element distribution coefficient varies with pH as shown by curve (R) in Figure 1.
The change of electrostatic forces at the adsorbing surfaces in the plume environment, due to the intrusion of chemically different water, causes the generation of the contaminant roll front in two ways:
- When sulfate anions desorb from the goethite surtaces due to the reduced sulfate concentration in the intruding water, the concentrations of the adsorbed cations decrease due to the reduced electrostatic attraction between the (fewer) sulfate anions and the cations. Of these cations the protons are most relevant for front generation.
- A fraction of the released protons is not complexed by proton buffers in the system and thus increases the proton activity of the pore water (i.e., decreases the pH).
Therefore, the Kd of the waste elements changes for two reasons:
- reduced electrostatic attraction (effect (3), above), and
- increased competition between protons and the contaminant for adsorption (effect (1), above).
Prior to the intrusion of the water, Kd is 20, after the intrusion, behind the pH front, at pH = 5.9, it is 0.2 (note that the dimensionless distribution coefficient, Kd = R - 1, is used here). These values can be taken either from Figure 1 or Figure 2.
At locations where the proton pool on the goethite surfaces is exhausted by leaching with intruding water, the pH goes back up to the pH of the incoming water, pH = 7 (see pH increase at locations 1 and 2 at time step 21).
The soluble contaminant concentration in the roll front is of the same order of magnitude as the adsorbed concentration, (i.e., about two orders of magnitude larger than the original soluble concentration in the undisturbed plume). The latter (Cw = 4.7 10-10 M) is the breakthrough concentration which constant Kd models would give us as maximum soluble contaminant concentration in the plume.
Not only is the soluble contaminant concentration larger than constant Kd models predict, the contaminant migration velocity is also larger when a roll front develops. The velocity of the contaminant roll front is given by Kdf . In the example displayed in Figure 2, it is approximately an order of magnitude larger than the velocity given by the constant Kd model (retardation factor of front is nearly unity, the one of the contaminant before remobilization is 20).
The steeper the spatial Kd profile of the contaminant across the remobilizing front, the higher is the resulting contaminant concentration in the roll front. An example for an environment with steep contaminant Kd profile is simulated in Figure 3.
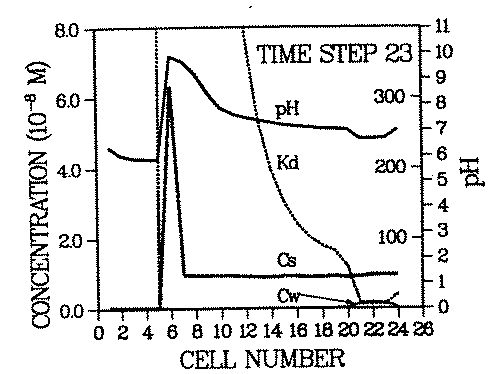
FIGURE 3:Generation of a secondary contaminant repository: This figure is time step 23 of a remobilization scenario identical to the one in Figure 2. with the exception that calcite is assumed to be present (in addition to goethite) in cell 6 at all times (0 - 23). The intruding water dissolves some calcite. This process consumes protons, thus raising the pH of the water downstream from cell 6. The result is the immobilization of the pH and Kd fronts for the period during which calcite is present. The contaminant roll front has migrated through cells 1 - 5, has carried the entire contaminant plume and deposit inventories of cells 1 - 5 into cell 6 and got trapped there. Cell 6 has become a secondary deposit (or repository) which will act as an enhanced contaminant source once the pH buffer (calcite) has been totally dissolved.
The remobilizing ion is the proton, like in Figure 2, but in this case the pH of the environment is buffered by the presence of calcite (calcite is present in cell 6). As long as this mineral exists, the incoming or desorbed protons will be consumed in the calcite dissolution process. Only after all calcite has been dissolved, will the pH drop abruptly and the contaminant roll front advance. One can see that due to the buffering of the pH and the corresponding fixation of the Kd front at cell 6, the inventory of cells 1 - 6 has been accumulated in cell 6.
Relationships between buffers, Kd profiles and the degree of accumulation have yet to be investigated. The former two are functions of the parameters listed in Table 1. It is apparent from the presented discussion that many of those parameters are sufficiently variable with time to cause considerable accumulations. It is also obvious that the state-of-the-art geochemistry will be especially interesting for impact assessments of long lived radionuclides.
In the following part of this paper, transport scenarios will be constructed, the conservatism of which would have been unjustified prior to the new insight into the influence of geochemical processes on contaminant transport exemplified in Figures 1, 2 and 3. Scenarios will be presented which provide the input values for a specific activity approach, the latter being used to evaluate the capability of geochemical processes in the biosphere of keeping neutron activated waste out of the food chain.
2.C Scenarios
Possible temporal variations of the environment are often called scenarios, but here the term will be used in a more general sense.
Two groups of scenarios can be distinguished.
- In the first, it is assumed that some behavior of the radionuclide can be modeled using a deterministic model (''deterministic scenarios").
- Scenarios of the second kind are not built exclusively on that assumption. They use available models to a varying degree to find natural analogs of the radionuclide migration to be considered ("natural analog scenarios").
Deterministic scenarios specify the temporal variations of model and environmental parameters, such as given in Table 1. Model parameters for real environments are often not available. Therefore, at present, those deterministic geohydraulic/geochemical transport computations will mainly help in designing and interpreting experiments which aim at identifying environments that cannot be described by the simpler constant or stochastic Kd models. Another use of deterministic scenarios is to calculate extreme behavior for which all data are available. This will be done in the last example below.
In natural analog scenarios, part of the information necessary to describe the fate of the radionuclide is taken from observation of environments that are considered natural analogs. For example, instead of calculating possible pollutant accumulations in non-constant Kd environments, the concentration spectrum of the element of concern is taken from analyzing environments which are similar to the one around the repository. Whether or not two environments are similar can be based on geochemical models. If the key transport parameter in two environments (e.g., the Kd of the pollutant)
- has similar values and
- varies similarly with the chemical composition of the pore water,
the environments may be considered analogs of each other.
This discussion emphasizes the fact that for environments to be analogs of each other, they must meet conditions 1 and 2. Condition 2 is neglected automatically when the constant or stochastic Kd approach is chosen. Then the resistivities of the environments against roll front formation are not compared.
For risk estimates, it wouid be desirable to know the range of pollutant concentrations that can be generated over the lifetime of a radionuclide by reconcentration processes such as roll fronts (or precipitation). That is beyond what current geochemical models can accomplish.
- Nevertheless, two, probably conservative, assumptions allow to construct a natural analog scenario that will provide probable upper limits of those concentrations as a potential starting point for the evaluation of natural geochemical barriers in soils (see section 3 A.).
- A deterministic geochemical model is then used to give an example of a possible refinement of the results of the first approximation (see section 3 B.).
3. APPLICATIONS
3 A. Use of Natural Analog Scenario to Classify Activated Waste
The following assumptions may provide the mentioned basis for the scenario:
- The average concentration range of element M in common soils of a large enough area is the result of only local spatial redistribution processes within the area: on the average no mass of M entered or left the environment (see references (31) and (32) for common examples in natural environments) .
- Those redistribution processes are entirely determined by geochemical and mineralogical parameters of the background and by the chemical interactions which M is subject to in this background environment (33). Examples of such parameters are the primary variables of Table 1 or such derived parameters as the steepness and velocity of the migrating Kd front and the velocity of the pollutant roll front. The resulting concentrations of M are thus independent from the initial concentration of M, (e.g., in the bedrock).
Both assumptions overestimate the extent of reconcentration of waste elements M, because
The exposure scenario is:
- waste molecules M have ''forgotten'' their origin and behave like the natural molecules M present in the plume environment.
- The concentration of waste element M on soil particles lies within the range of natural concentrations of M in the considered environment.
- Biota access location is an aquifer contaminated with M. Water differing in chemical composition from the composition of the original pore water of the aquifer intrudes and remobilizes M. A roll front is generated. Consistently with assuming that 2. describes a long term equilibrium state, the soluble inventory of M in the pores is taken to be less than or equal to the inventory of M associated with the solid matrix prior to remobilization.
- The contaminated water is consumed as drinking water, and no other source of drinking water is used. The waste inventory in the aquifer is large enough to contaminate the water supply of the exposed group for a year (730 liter per person). This assumption about the waste inventory typically holds for elements activated in the region between the reactor core and the innermost layers of the bioshield.
The corresponding waste element intake in one year is
mM = 730 (L/yr) x 10 (kg/L) x Cs (mg/kg) ................... [8]
Notation
where 10 Cs is the concentration in the pore water after the inventory of M on the solid soil matrix has been remobilized, assuming a solid/solution ratio of 10 kg/L (equivalent to a bulk density of the soil of ρ = 1.8 g/cm3 , and a minimum porosity of 0.2).
The reference intake is the one that leads to the reference level of radiation dose:
mp = Cp m = 0.1 ALI/S(t) ................... [9]
Notation
where Cp is taken from Eq. 1.
If the assumptions in the radiological model are chosen appropriately and the reference exposure level represents a societally accepted limit, an environment will be considered to have isolated the waste element if
mM < mp ................... [10]
Notation
Whether or not Eq. 10 is the case depends on the specific activity of M. For the elements of interest here, the specific activity is a linear function of the neutron dose D (cm-2 ) to which M has been exposed:
S(0) = 3.5 10 -22M f σ D/(MT) ................... [11]
Notation
where
f is the natural abundance (fractions of one) of the mother isotope,
M (gram) is the molecular weight of the waste element M, and
σ (barn) is the thermal neutron capture cross section for the activation of the waste radionuclide from the mother isotope.
T (yr) is the radionuclide half life.
The factor 3.5 10-22 converts the dimension of S(t=0) to Curie/mg.
The neutron dose Dp for which the equality in Eq. 10 holds is the upper limit below which the biosphere environment is able to keep M within legally acceptable isolation. Combining Eqs. 8, 9 and 11 gives an expression for the characteristic ratio mM /mp
mM /mp = 730 x 10 x 3.5 x 1O-22f D Cs σ / (0.1 M T ALI) ................... [12]
Notation
Equation 12 is evaluated for each element of the periodic table from hydrogen to bismuth,
- in which a long lived (T >10 yr) daughter is generated by thermal neutron capture processes,
- of which the concentration range in common soils has been reported. Cs is the upper limit of that range.
The data used in these screening calculations are taken from references (34 - 36) and are listed in Table 2.
TABLE 2:
Data used to calculate maximum thermal neutron dose, Dp.
Element
(Radionuclide) |
T
(yr) |
σ
(barn) |
ALI
(Ci/yr) |
Cs
(mg/kg) |
| Ag (108Ag*) a |
1.3 10+2 |
3.0 10+0 |
8 10-4 |
5 10+0 |
| Ba (133Ba) |
1.1 10+1 |
8.5 10+0 |
2 10-3 |
3 10+3 |
| Be (10Be) |
1.6 10+6 |
9.2 10-3 |
2 10-5 |
4 10+1 |
| C (14C) |
5.7 10+3 |
9.0 10-4 |
6 10-3 |
2 10+4 |
| Ca (41Ca) |
1.3 10+5 |
4.0 10-1 |
2 10-3 |
5 10+5 |
| Cd (113Cd*) a |
1.5 10+1 |
6.0 10-2 |
2 10-5 |
7 10-1 |
| Cl (36Cl) |
3.0 10+5 |
4.3 10+1 |
2 10-3 |
9 10+2 |
| Mo (93Mo) |
3.5 10+3 |
5.0 10-2 |
3 10-3 |
5 10+0 |
| Nb (94Nb) |
2.0 10+4 |
1.2 10+0 |
1 10-3 |
7 10+1 |
| Ni (59Ni) |
7.5 10+4 |
4.6 10+0 |
3 10-2 |
5 10+2 |
| Ni (63Ni) |
1.0 10+2 |
1.4 10+1 |
1 10-2 |
5 10+2 |
| Pb (205Pb) |
1.4 10+7 |
6.0 10-1 |
3 10-3 |
2 10+2 |
| Se (79Se) |
6.5 10+4 |
5.3 10-1 |
2 10-3 |
2 10+0 |
| Sn (121Sn*) a |
5.0 10+1 |
1.0 10-3 |
2 10-3 |
2 10+2 |
| Zr (93Zr) |
1.5 10+6 |
2.6 10-1 |
2 10-3 |
2 10+3 |
Legend:
a designates metastable state.
sources:
σ: reference (34).
ALI: reference (6).
Cs: reference (35), except for Nb.
Cs of Nb calculated from intake rates (ref. 5) and transfer factors in food chain (ref. 36):
Cs = u/[Biv(mv + 50(Fw mM + Fl ml)]
where:
u ................... element intake rate: 230 mg yr (ref. 5),
Biv ................... transfer coefficient from soil to plant: 9.4 x 10-3 kg soil/kg plant,
mp ................... consumption rate of plants by man: 584 kg plants per year.
50 ................... consumption of grass by cow: 50 kg per day,
FM ................... transfer coefficient from grass to milk: 2.5 x lO-3 day/L
mM ................... consumption rate of milk by man: 310 L/yr.
Fl ................... transfer coefficient from grass to meat: 2.8 x 10-1 day/kg .
mf ................... consumption of meat by man: 110 kg/yr.
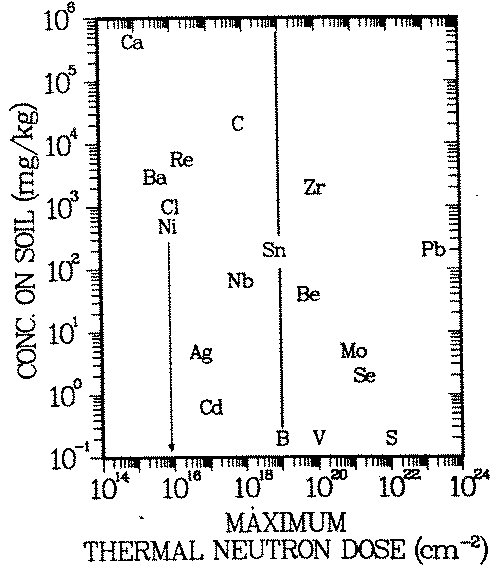
FIGURE 4: Natural analog scenario: Geochemical isolation of long lived activation products (T > 10 yr) in common soils. Exposure pathway: drinking water. The diagram gives the upper limit of the thermal neutron irradiation to which an element may be exposed and still be ''sufficiently" attenuated in common soils. Example: Nickel may receive a dose of approximately 1016 thermal neutrons per square centimeter. The maximum nickel concentration in common soils is 500 ppm. See assumptions 1 -3 in radiological model for interpretation of the term "sufficient". B, V, S are neutron doses at the inner surfaces of the bioshield, reactor pressure vessel wall and in the reactor core, respectively.
In Figure 4 the element symbols (e.g., Ni, Ca) are entered in Cs-D space where mM /mp = 1. This graphical representation combines one hazard index of each of the three involved models in the term Cs σ/ALI. Elements for which this term is highest (e.g., Ca, Cl, Ni, or C) become hazardous already after modest neutron irradiation (for Ni: 1016 neutrons/cm2 ), because the environmental geochemistry does not seem to be able to limit their concentrations to small enough levels. The neutron irradiation regime in a reactor is indicated on the abscissa: B and V mark the doses at the inner surfaces of the bioshield and pressure vessel, respectively, and S the one at the center of the core.
Accumulation processes, such as roll fronts, seem not to be able to open up the "cage" in which the geochemistry in common soils keeps activated lead isolated from the food chain. Only irradiation with a neutron dose exceeding 1023 neutrons/cm2 (an order of magnitude more than available in power reactors) will lead to excessive releases from geochemical barriers present in soils.
The situation is similar for some elements activated in the most bulky part of the reactor, the biological shield: Se, Mo, Be, Zr, and Sn, activated in the bioshield, are locked up in a ''geochemical cage''. On the other hand, elements to the left of the vertical line in Figure 4 are probably not sufficiently isolated by the processes described aboves
The time after which assumption 1 of this scenario is valid (''waste residence time'') is possibly another geochemical barrier enhancing the isolation provided by the geochemistry described in sections 2.A and 2.B. For example, if it takes 1000 years for a waste element to reach common soil concentrations in remobilization/redeposition cycles, its radioactive isotopes may have decayed to insignificant values by then. The elements barium, silver, cadmium and tin could fall in that category, because their radioisotopes generated by thermal neutron irradiation have half lives smaller than 150 years. After 1000 years, their specific activities will have decreased by radioactive decay by three orders of magnitude or more. Thus, mp and correspondingly Dp would be three orders of magnitude larger. Ther symbols of those elements would therefore have to be entered three or more decades further to the right. Silver, cadmium and tin would then lie to the right of the vertical line ib Figure 4, i.e. after activation in the biological shield they would still belong to the class of elements contained in the "geochemical cage" mentioned above.
Figure 4 allows the discussion of the influence of major parameters, i.e. of
- the potential for reconcentration of the waste element in the considered soil,
- the resistance of the soil against remobilization, and
- the coupling between food pathway and soil.
Factors (a), (b) and (c) are fixed in assumptions 2, 3 and 4 of the exposure scenario, respectively, and represented by the three terms in Eq. 8.
Factor (a) is reflected in the value 10 kg/L which implies that the entire solid inventory of waste element M is assumed to become remobilized from the solid matrix of the porous medium into its pore water when the system is perturbed by intrusion of water from outside. As has been shown in Figure 1, in the case of an adsorbed contaminant total remobilization (Kd = 0, R = 1) is not the only possible reaction of the system to a change of the chemical pore water composition. Normally, changes of Kd with changes of the major ion concentrations are less than one order of magnitude and typically one to two orders of magnitude per unit pH change. For such cases of incomplete remobilization Eq. 8 has to be modified by replacing 10 kg/L with (10/R) (kg/L) where R is the retardation factor after change of the pore water composition.
It is known that the inventory of an element associated with the solid matrix of the soil is distributed among various mineral phases (see e.g., sum over k in Eq. 5). These minerals react differently to changes in the pore water composition (e.g. some are stable when the pore water changes within certain limits). Thus, only a fraction r < 1 of Cs might have to be considered in Eq. 8.
Similarly, the coupling between soil and food chain might not be as strong as assumed in 4 of the exposure scenario, and term 730 would have to be replaced with a smaller one. The correspondingly modified Eq. 12 would be:
mM /mp = 730 r x 10/R x 3.5 x 10-22 f D r Cs σ / (0.1 M T ALI)................... [12']
Notation
- To represent cases with R and r different from 1 graphically in Figure 4, each element symbol (e.g., Ni, Ca) needs to be replaced with a straight line starting at the location of the symbol and running downwards with a slope of -1. Its starting point represents the conservative case R = 1, r = 1.
- Different soil/food coupling leads to a shifting of the line parallel to the one through the location of the element symbol.
Whenever a line crosses the vertical line in Figure 4, the corresponding element is one of those activated elements in the bioshield which the biosphere environment "can isolate". When a line crosses a vertical line running through S, the environment "can isolate" the element regardless of where in the reactor it has been activated.
3 B. Use of Natural Analog and Deterministic Scenarios to Calculate Potential Impact of Activated Nickel
The discussion in Figure 4 was concerned with a broad spectrum of elements and whether or not one specific environment, the common soil, is able to "isolate" those elements. The last part of this paper will do the reverse. It will discuss one major waste element and address the question which environments are able to "isolate" it.
Of the elements in Figure 4 that have the highest combined hazard index Cs σ/ALI calcium, nickel, carbon and niobium are major or minor constituents of the reactor materials steel and concrete. The others in Figure 4 with high hazard index are trace components.
The biological hazard potential is the ratio of the total activity and Cp. It has been a commonly used measure of the inventory of a radionuclide in a reactor or repository. For a long period of time the potential risks of activated stainless steel and concrete are almost identical to their nickel and calcium content (3, 38, 39, 57). Of those two major waste elements nickel will be chosen for the discussion of the last subject.
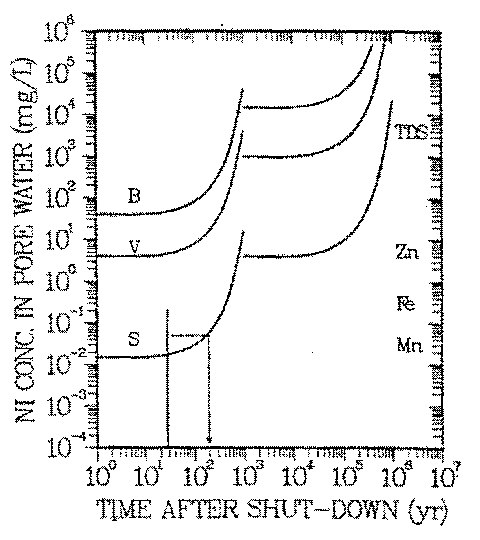
FIGURE 5: Natural analog scenario: Geochemical isolation of nickel in natural waters. Exposure pathway: drinking water. Vertical line: range of natural concentrations of nickel. B-, V-, S-Curves: reference concentrations Cp(t), Eq. 1. See Table 3 for data used in calculations of Cp(t=0).
The curves give the increase of the reference concentration with radioactive decay time for nickel activated at three representative locations within a pressurized water reactor. When Cw of a location lies above the curve, the natural isolation in this environment is insufficient. Example: Environments in which the maximum soluble nickel concentration is 0.05 mg/L provide ''sufficient'' isolation tor nickel activated near the center of the reactor core if the waste is kept isolated in a repository for 200 years (see arrow). Only nickel activated near the reactor core (curve S) needs to be kept behind repository barriers until its activity has decayed sufficiently. The symbols on the right margin give taste thresholds for soluble manganese, iron and zinc, and any combination of natural anions and cations (TDS). If the soluble concentration exceeds those thresholds, the water has an unpleasant taste. For details of the term ''sufficient" see description of metabolical model.
TABLE 3
Reference concentrations of nickel in drinking water
calculated from specific activity S(t = 0), see Eq. 1.
(values in upper row are valid after decay of 63Ni, appoximately after 1000 yr,
those in the lower row are valid prior to that time.)
Location in Reactor:
Inner Surface of ... |
S(t = 0)
(Ci/mg)
|
Cp(t = 0)
(mg/L)
|
Radioisotope |
| bioshield |
4.1 x 10-4
4.9 x 10-2 |
1 x 10+4
4 x 10+1 |
59Ni
63Ni |
| pressure vessel |
3.9 x 10-3
4.6 x 10-1 |
1 x 10+3
3 x 10+6 |
59Ni
63Ni |
| shroud |
9.1 x 10-1
1.5 x 10+2 |
4 x 10+0
1 x 10-2 |
59Ni
63Ni |
Legend
Sources:
σ from reference (34),
D (see Eq. 11 for S(t=0)) from reference (37),
m = 730 L/yr,
operation time of reactor at full power: 30 yr
Figure 5 allows to compare observed concentrations of nickel in water, Cw (vertical line on the left side of Figure 5), and Cp(t) for the above mentioned locations S, V, and B within the reactor. The left hand branches of the Cp curves represent the radiological effects of 63 Ni, the right hand ones those of 59 Ni. Because the specific activity of 63 Ni is two orders of magnitude larger than the one of 59 Ni and its ALI is a factor of two smaller than the one of 59 Ni, the risk of activated nickel is controlled by 63 Ni. This is the case for about 1000 years. In Figure 5
Each of the irradiation positions S, B, and V is represented by a Cp curve, the curve for the most intense neutron irradiation (location S) being the lowest one. Nickel in activated steel, classified as class C waste acceptable for land disposal (40) would be represented by a Cp curve close to curve S.
The range of observed nickel concentrations in some surface- (41) and groundwaters (42) of the United States is represented in Figure 5 by the vertical line. Assuming that those waters are analogs of long term waste nickel plumes (natural analog scenario described by (a), (b), and 1., and exposure scenario 4. of 3.A) leads to interesting consequences: Typical nickel concentrations in aquifers (Cw < 10 ng/L) are below Cp, regardless of where in the reactor nickel has been activated. Only nickel concentrations in the upper end of the environmental concentration spectrum are higher than Cp and only if nickel has been exposed to the intense neutron fluxes of the reactor core (curve S). Such activated nickel contains 63 Ni in excess of that to be retained by the natural water chemistry. The period during which that is the case is ten half lives of 63 Ni as mentioned above (see arrow in Figure 5).
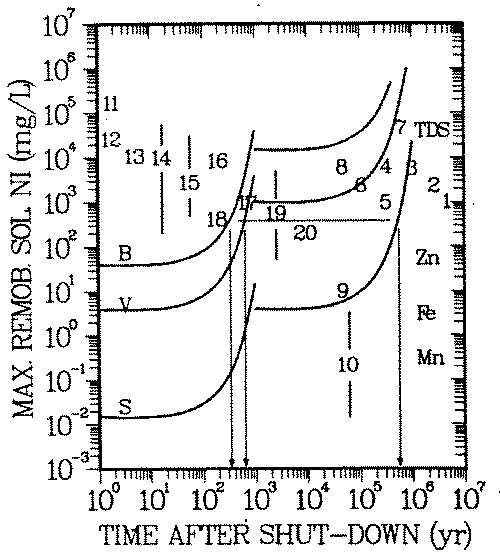
FIGURE 6: Natural analog scenario: Geochemical isolation of nickel in soil environments. Exposure pathway: drinking water. B-, V-, S-Curves: reference concentrations Cp(t), same as in Figure 5. Numbers: Symbols for environments (see Appendix B for explanation) Symbol for an environment is located at Cw, Eq. 13.
When a symbol lies above the curve, the geochemical isolation is insufficient. Example: Remobilization of nickel from soils of environment 18 (river sediments) could result in a nonacceptable soluble concentration for a period of 300, 600 and 600,000 years after shut-down of the reactor, if the nickel was activated in the bioshield (B), pressure vessel wall (V) and the reactor core (S), respectively. This nickel concentration is above some of the known taste threshold and may be noticeable as unpleasant taste of the water.
Figure 6 contains the reference concentrations Cp(t) and concentrations Cw which develop in the natural analog scenario (a, b, 1-4) described in section 3.A:
Cw = 10 kg/L x Cs ................... [13]
Notation
Input to this scenario is the concentration of nickel on the solid soil/rock phase, Cs. Concentrations Cs of a spectrum of 20 environments (43 - 52, Appendix B) have been considered. Concentrations 1 - 10 have been derived from adsorption capacities of single soil/rock mineral phases, thus being based on a deterministic scenario. Concentrations in environments 11 - 20 have been observed and are used as natural analogs. The highest nickel concentrations are to be expected in environments dominated by organic matter (7, 14, 15) and by iron oxides (5, 8, 11).
Figure 6 shows that above taste threshold remobilized concentrations are in the range 103 -105 mg/L. Accordingly the biosphere might be "protected" from the long lived radioisotope of nickel, except when it has been generated in the high neutron flux region of the reactor. Under the conditions described in this paper, repositories would need to provide isolation against the 63 Ni content in the corresponding materials for a period of less than 1000 years (see arrows in Figure 6).
Based on the above mentioned roll front scenario the concentration of nickel from class C activated steel might be higher than acceptable for up to 106 years (see arrow in Figure 6). If physical dilution cannot take place for this period, corrosion products of that highly an activated steel structure must not come in contact with the considered soil phases or enter into any of the environments 1 -20, if roll front formation of the type of Figure 2 and 3 cannot be excluded in those environments.
Water having a concentration of dissolved species above 2000 mg/L (see TDS level in Figure 5 and 6) is currently not used in the U.S. as drinking water. Furthermore, if the zinc, iron or manganese concentration exceeds the corresponding level shown in Figs. 5 and 6, the water has an unpleasant "metal taste" (53). These four concentration levels can be taken as a guide for a corresponding nickel concentration threshold: if the water has a nickel concentration exceeding this threshold, it will probably not be used as drinking water.
Not only this "taste barrier" might isolate activated nickel. A far more effective barrier is the water chemistry, as might be expected comparing Figure 5 and 6 This barrier has been deliberately eliminated in assumption 3. of the roll front scenario.
Soluble equilibrium concentrations of M reach an upper limit when the water becomes saturated with. respect to a mineral containing M ("water chemistry barrier''). Figure 7 contains all of the presently available quantitative geochemical information on nickel minerals and soluble nickel complexes in inorganic environments (38) (i.e., where chemical processes due to organic matter are negligible).
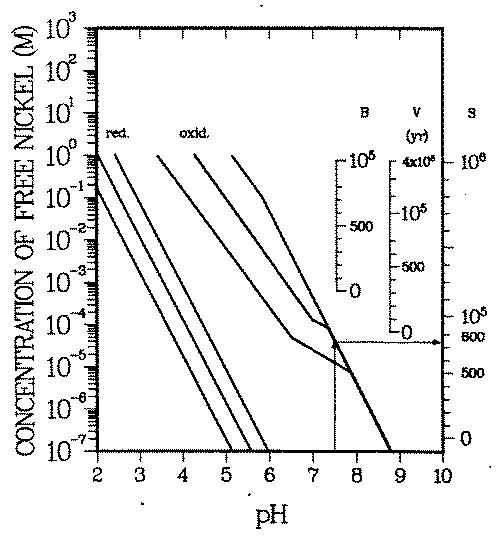
FIGURE 7: Deterministic geochemical scenario: Time during which nickel activated at representative locations B, V, S (see Figure 6) in reactor has to be isolated before it can be released into drinking water supplies which do not contain organic complexing agents. These necessary isolation times can be read off the right ordinates. The water is assumed to be saturated with nickel. Each curve triplet bounds the range of possible nickel concentrations. One triplet applies to reducing and the other to oxidizing environments. The center curves of each group give the most probable concentrations. The soluble concentrations have been converted into necessary isolation times, expressed in years after shutdown. Example: At pH = 7.5 nickel concentrations in oxidizing drinking water are below ''permissible'' concentrations, if the nickel was activated in the bioshield (B) or pressure vessel wall (V). If the nickel was activated in the reactor core (S), it needs to be kept out of the water supplies for at most 750 years. Reducing waters will ''sufficiently" isolate nickel activated anywhere in the reactor.
Oxidizing and reducing environments have different stable mineral phases, nickel sulfide in reducing whereas nickel phosphate and nickel hydroxide in oxidizing environments. The ligand concentrations (sulfide in reducing, phosphate in oxidizing environments, apart from the proton) influence the concentration of the free nickel ion in equilibrium with the minerals. In Figure 7, the center line in each group of curves gives the concentration of free nickel at common sulfide and phosphate concentrations, respectively, the two lines right and left of the center line specify the possible range of free nickel concentrations for reasonable ligand concentration variations (see Table 4 for details).
TABLE 4
Data used to calculate maximum free nickel concentrations
in equilibrium with minerals (references in parentheses)
| (I) Mineral Solubilities |
| Mineral |
Precipitation Reaction |
logK (Ref.) |
| NiS |
Ni2+ + S2- = NiS |
-21.0 (54) |
| Ni3(PO4)2 |
3 Ni2+ + 2 PO42- = Ni3(PO4)2 |
-31.3 (21) |
| Ni(OH)2 |
Ni2+ + 2 H2O = Ni(OH)2 + 2 H+ |
10.8 (24) |
| (II) Natural Variation of Ligand Concentrations |
| Ligand |
Logarithm of Concentration Range
(C in mol/L) |
Reference |
| S |
-4.5 .... -6.5 |
(a) |
| PO4 |
-3.2 .... -6.2 |
(42) |
Legend
(a) Upper concentration limit in drinking water given be "rotten egg" smell, lower concentration limit arbitrarily chosen to lie at 1 percent cumulative frequency value for major ions in terrestrial waters (55).
1 percent cumulative frequency value means: 1 percent of the waters have concentrations not exceeding this value.
For example (see arrow in Fig. 7), at pH = 7.5 the equilibrium concentration of the free nickel ion in oxidizing environments cannot exceed 5.0 10-5 M (= 3 mg/L). In reducing environments precipitation of nickel starts at a free nickel concentration orders of magnitude below the one in oxidizing environments.
In inorganic environments the concentration of soluble nickel complexes is at most of the same order of magnitude as the one of free nickel (38). Complexation can thus be neglected here, for simplicity (i.e., Cw = [Ni2+ ] is assumed). Because the natural concentrations in Fig. 5 have all been observed in inorganic environments, it is not unexpected that they lie below the lines of Fig. 7.
As in the previous figures, the solution of the equation Cw = Cp(t) for t gives the life times of repository barriers needed as supplement to the natural geochemical barriers when Cw exceeds Cp(t = 0):
t = T / ln2 (ln Cw - ln Cp(t = 0)) ................... [14]
Notation
t has been entered as right ordinate in Fig. 7. Because t is a function of the activating neutron flux, there is one ordinate for each of the three representative radial locations within the reactor.
As can be seen, the nickel minerals are probably insoluble enough at pH > 7.5 to ''isolate" nickel activated in the largest parts of the reactor structure. Concentrations Cw, as given by the extreme roll front scenarios, can only develop in acid environments or in the presence of strongly complexing organic agents.
4. CONCLUSIONS
A monotonic decrease of contaminant concentration with distance from the repository, the result of present day transport calculations, seems to be only one special case of migration. In general, the superposition of hydrodynamic processes (physical processes affecting the macroscopic and microscopic soil parameters), of physico-chemical processes and chemical reactions leads to spatial fluctuations of contaminant concentrations in soil (secondary repositories). Changes of the major ion concentrations by infiltration of water differing in chemical composition from the one originally present propagate through the soil system with their own parameters governing transport. Migration of a contaminant in such a changing environment does not follow the predictions of models which are based on the assumption of a constant Kd or a spectrum of stochastic Kd's.
A typical contaminant transport process in such environments is the roll front. Model calculations show that they are able to migrate
- faster than the contaminant in the original undisturbed system, and
- that they do not generally decrease in concentration as they migrate.
They are thus able to build up a secondary repository at the biota access location.
As long as observed spatial fluctuations have not been systematically interpreted using geochemical models, potential upper concentration limits in such fronts could be inferred from analog environments, especially when the life time of the involved radionuclide is long.
In a first attempt, such upper limits of concentrations on the solid soil matrix can be linked to radionuclide intake via scenarios which seem to be very conservative as far as we know. Such an assessment shows that the soil chemistry protects man against a number of radionuclides similarly as against stable toxic substances in the biosphere. Examples are beryllium, zirconium, molybdenum,
selenium and lead activated outside the reactor pressure vessel.
When the barrier provided by solubility limits of the contaminant (in water) is no longer neglected (that was done in the above conservative scenarios), the list of activation products isolated by geochemistry gets larger. This barrier seems to provide protection against nickel activatwed even within the reactor pressure vessel wall, if the pH of the water does not drop below 7.5. Nickel is a major contributor to long lived waste in activated reactor structure.
The proposed use of a combination of geochemical transport models and scenarios allows to calculate the residual isolation time. This is the time during which the radioactive waste has to be kept confined in a repository, because its activity is too high to be sufficiently isolated by geochemical processes alone. For nickel activated outside the reactor pressure vessel (i.e., in the bulk of the reactor decommissioning waste), residual isolation times range from several hundred years to thousand years only in acid or strongly complexing environments.
REFERENCES
1. Office of Nuclear Matelial Safety and Safeguards. Draft Environmental Impact Statement on 10 CFR Part 61, Licensing Requirements for Land Disposal of Radioactive Waste. NUREG-0782, Nuclear Regulatory Commission, Washinigton, DC (1981).
2. Bell, M. J. ORIGEN - the ORNL isotope generation and depletion code. ORNL-4628 Oak Ridge National Laboratory Oak Ridge, TN (1973).
3. Gruber, J.. Lehmann, B., and Schneider. J. NUCCON - A program for calculating the neutron activation. HMI-B 312, Hahn-Meitner-lnstitut fuer Kernforschung, Berlin, Germany (1979).
4. ICRP Publication 23, Task group on Reference Man. Pergamon Press, Oxford, United Kingdom (1975).
5. ICRP-Publication 26, Recommendations of the International Commission on Radiological Protection. Pergamon Press, Oxford, United Kingdom (1977).
6. ICRP-Publication 30, Annual limits for intake of radionucludes by workers. Annals of the ICRP 2 and 4, Pergamon Press Oxford, United Kingdom (1979), (1980).
7. Kent, D. B., Tripathi V. S., Ball, N. B., and Leckie, J. O. Surface complexation modeling of radionuclide adsorption in sub-surtace environments. Tech. Report No. 294, Sandia National Laboratories, Albuquerque, NM (1986).
8. Nordstrom, D. K. and Ball, J. W. Chemical models. computer programs and metal complexation in natural waters. In: Proc. Int. Symp. Complexation of Trace Metals in Natural Waters, C. J. M. Kramer and J. C. Duinker, eds., May 2-6, 1983, Texel, The Netherlands, Martinus Nijhoff/Dr. W. Junk Publishers (1984).
9. Jennie, E. A. Waste/rock interactions technology program, geochemical modeling: A review. PNL-3574, Pacific Northwest Laboratories, Richland, WA (1981).
10. Davis, J. A. and Leckie. J. O. Surface ionization and complexation at the oxide/water interface. J. Colloid. Interface Sci. 63: 480 (1978) and 74: 32 (1980)
11. Westall J., Zachary, J. L., and Morel, F. M. M. MINEQL, a computer program for the calculation of chemical equilibrium composition of aqueous systems. Mass. Inst. of Tech., Dept. Civil Engineering, Tech. Note 18 (1976).
12. James, R. O. and Parks, G. A. Characterization of aqueous colloids by their electrical double-layer and intrinsic surface chemical properties. Surf. Coll. Sci. 12: 119 (1982).
13. Hingston, F. J., Posner, A. M., and Quirk, J. P. Adsorption of selenite by goethite. In: Adsorption from Aqueous Solution, W. Weber and E. Matijevic, eds., Adv. Chem. Ser. No. 79: 82 (1968).
14. Sposito, G. Surface Chemistry of Soils. Oxford University Press, Oxford, United Kingdom (1984).
15. Balistrieri, L. and Murray, J. W. Surface of goethite (alpha-FeOOH) in sea-water. In: Chemical Modeling of Aqueous Systems, E. A. Jenne, ed., Am. Chem. Soc. Symp. Ser. 93: 275 (1979).
16. Balistrieri, L. S. and Murray, J. W. The surface chemistry of goethite (alpha-FeOOH) in major ion sea water. Am. J. Sci. 281: 788 (1981).
17. Richter, R. O. Chemical speciation of fly ash leachate in the underlying soil/water system with emphasis on the adsorption of nickel by oxides. Ph.D. dissertation, University of Notre Dame, IN (1978).
18. Ball, J. W., Nordstrom, D. K., and Jenne, E. A. Additional and revised thermodynamic data and computer code for WATEQ2 - a computerized chemical model for trace and major element speciation and mineral equilibria of natural waters. U.S. Geol. Surv. Water Resour. Invest. 78 (1980).
19. Truesdell, A. H. and Jones, B. F. WATEQ, a computer program for calculating chemical equilibria of natural waters. Jour. Research U.S. Geol. Surv. 2:233 (1974).
20. Stumm, W. and Morgan, J. J. Aquatic Chemistry, 2nd ed. John Wiley, New York (1981).
21. Wagman, D. D., Evans, W. H., Parker, V. B.. Halow, I. Bailey, S. M., and Schumm, R. H. Selected values of chemical thermodynamic properties. Institute for Materials Research, National Bureau of Standards. Technical Notes 270-3 and 270-4, Washington, DC (1969) and (1971).
22. Mattigod, S. V. and Sposito, G. Estimated association constants for some complexes of trace metals with inorganic ligands. Soil Sci. Soc. Am. J. 41: 1092 (1977).
23. Sillen, L. G., Martell, A. E. Stability Constants of Metal-lon Complexes. The Chemical Society, London, Special Publication 17, and Supplement No. I (1964) and (1971).
24. Baes. C. F., Jr. and Mesmer, R. E. The Hydrolysis af Cations. John Wiley, New York (1976).
25. Jenne. E. A. Controls on Mn, Fe, Co, Ni, Cu and Zn concentrations in soils and water: The significant role of hydrous Mn- and Fe-oxides. Adv. Chem. Ser. 73: 337 (1968).
26. Rai, D., Zachara, J. M., Schwab, A. P., Schmidt, R. L. Girvin, D C., and Rogers, J. E. Chemical attenuation rates, coefficients and constants in leachate migration, Vol. 1: A critival review. EPRI EA-3356, Vol. 1, Electric Power Research Institute, Palo Alto, CA (1984).
27. Granger, H. C. and Warren, C. G. Unstable sulfur compounds and the origin of roll-type uranium deposits. Econ. Geol. 64: 160 (1969).
28. Killey, R. W. D., et al. Subsurface cobalt-60 migration from a low-level waste disposal site. Environ. Sci. Technol.18: 148 (1984) .
29. Serne, R. J., Peterson, S. R., and Gee, G. W. Laboratory measurements of contaminant attenuation of uranium mill tailings leachates by sediments and clay liners. NUREG/CR-3124, PNL-4605, Pacific Northwest Laboratories, Richland, WA (1983).
30. Peterson, S. R., Martin, W. J., and Serne, R. J. Predictive geochemical modeling of contaminant concentrations in laboratory columns and in plumes migrating from uranium mill tailings waste impoundments . NUREG/CR-4520, PNL-5788, Pacific Northwest Laboratories, Richland, WA 99352 (1986).
31. Mollitor, A. V. and Raynal, D. J. Acid precipitation and ionic movement in Adirondack forest soils. Soil Sci. Soc. Am. J. 46: 137 (1982).
32. Van Breemen, N. and Brinkman, R. Chemical equilibria and soil formation. In: Soil Chemisty. C. H. Bolt and M. G. M. Bruggenwert, eds., pp. 141-170. Elsevier, Amsterdam. A. Basic Elements. (1981).
33. Aubert, H. and Pinta, M. Trace Elements in Soils. Elsevier, Amsterdam, The Netherlands (1977).
34. Mughabghab, S. F. and Garber, D. 1. Neutron reaction cross
sections. BNL-325, Brookhaven National Laboratory, National Neutron Cross Section Center, 3rd. ed., Vol. I (1973).
35. Lindsay, W. L. Chemical Equilibria in Soils. John Wiley, New York (1979).
36. U.S. Nuclear Regulatory Commission. Calculation of annual doses to man from routine releases of reactor effluents for the purpose of evaluating compliance with 10 CFR Part 50, App.1. Regulatory Guide 1.109, Revised Edition (1977).
37. Smith, R. I., Konzek, G. J., and Kennedy, W. E. Technology, safety and costs of decommissioning a reference pressurized water reactor power station. NUREG/CR-0310, U.S. Regulatory Commission, Washington, DC (1978).
38. Gruber, J. and Tripathi, V. S. Potential equilibrium concentrations of nickel and molybdenum in groundwater as indicators for the necessary isolation of radioactive waste from INTOR. Final Report, INTOR/NET Study Contract 084/81-11/FU-DNET, Fusion Directorate, DGXII, Commission of the European Community, Rue de la Loi, Brussels, Belgium (1983).
39. Evans, J. C. et al. Long-lived activation products in reactor materials. NUREG/CR-3474, U.S. Nuclear Regulatory Commission, Washington, DC (1984).
40. 10 CFR Part 61, Licensing requirements for land disposal of radioactive waste. Code of Federal Regulations, Office of the Federal Register, National Archives and Records Administration, United States Government Printing Office, Washington, DC (1982).
41. Kopp. J. F. and Kroner, R. C. Trace metals in waters of the U.S. U.S. Dept. Interior, Fed. Water Pollution Control Administration, Div. of Population Surveillance, also published in: Drinking Water and Health, National Academy of Sciences, Washington, DC (1977).
42. Kansas Geological Survey Local quality of irrigation waters in West-Central Kansas. Chemical Quality Series 2, Lawrence, Kansas (1975).
43. Scheffer, F., Schachtschabel, P. Lehrbuch der Bodenkunde. Enke, Stuttgart, Federal Republic of Germany (1966).
44. Marshall, C. E. The physical chemistry and mineralogy of soils. In: Soil Materials, Vol. 1, John Wiley, New York (1964) .
45. Turekian, K. K. and Wedepohl, K. H. Distribution of elements in some major units of the earth's crust. Geol. Soc. Am. Bull. 72: 186 (1961).
46. Foerstner, U., Wittmann, G. T. W. Metal Pollution in the Aquatic Environment, p. 229, Springer, Berlin (1981).
47. Ogura, Y. Mineralogical studies on the occurrence of nickeliferous laterite deposits in the southwestern Pacific area. Min. Geol. 27: 379 (1977).
48. Worthington, J. E. An exploration program for nickel in the southeastern United States. Econ. Geol. 59:97 (1964).
49. Blakeslee, P. A. Monitoring considerations for municipal wastewater effluents and sludge application to the land. University Workshop, Champaign, Urbana, IL, U.S. Environmental Protection Agency and U.S. Department of Agriculture (1974).
50. Berrow, M. L. and Webber, J. Trace elements in sewage sludges. J. Sci. Food. Agric. 23: 93 (1972).
51. Erlenkeuser, H., Suess, E., and Willkomm, H. Industrialization effects: Heavy metal and carbon isotope concentration in recent Baltic Sea sediments. Geochim. Cosmochim. Actal 38: 823 (1976).
52. Patchineelam, S. R. Untersuchungen ueber die Hauptbindungsarten und die Mobilisierbarkeit von Schwermetallen in fluvialen Sedimenten. Ph.D. thesis, University of Heidelberg, Federal Republic of Germany (1975).
53. Sawyer, C. N., McCarty, P. L. Chemistry for Environmental Engineering. McGraw Hill, New York (1978).
54. Smith, R. M., Martell, A. E. Critical Stability Constants, Vol. 4: Inorganic Complexes. Plenum, New York (1976).
55. Davies, S. N., DeWiest, R. C. M. Hydrogeology Wiley, New York (1966).
56. Gruber, J. Contaminant accumulation during transport through porous media, Water Resour. Res., 26, 99 - 107 (1990).(updated version)
57. Gruber, J. High-level radioactive waste from fusion reactors, Environ. Sci. Tech. 17, 425 - 431, 1983. (updated version)
Acknowledgement
Part of this research was sponsored by the University of California at Riverside "Toxic Substances Research and Training Program'' and performed in the Environmental Science Group of Los Alamos National Laboratory.
Notation
ALl ................... the element dependent annual limit for intake of radionuclides by occupationally exposed workers given in (6) (Ci/yr),
B, V, S .............. the inner surfaces of the bioshield, reactor pressure vessel wall and in the reactor core, respectively,
Cs ................... concentration of M on solid phase (g of M per kg of soil),
Cp(t) ................... "reference" or "permissible concentration", concentration of waste element in food at which radioactive exposure is 0.5 rem/yr (mg of M per kg of food),
Cw ................... concentration of M in liquid phase (g of M per L of water),
D ................... thermal neutron dose (neutrons per cm2 ),
f ................... the natural abundance (fractions of one) of the mother isotope,
j ................... designates the pollutant element,
Kd ................... Cs/Cw (dimension L/kg), note that in the figures Cs is measured in mg per kg soil volume, and then Kd = 1 - R and is dimensionless
M ................... contaminant, typically nickel,
M ................... the molecular weight of the waste element M (g),
M ................... mole/L,
m ................... the annual consumption rate of contaminated food (kg/yr), food = water for drinking water exposure pathway,
mM ................... waste element intake per year (mg/yr),
mp ................... permissible ("reference") waste element intake per year (mg/yr),
n ................... effective porosity of soil (dimensionless),
σk ................... the side reaction coefficient for adsorption reaction,
σl ................... the side reaction coefficient for formation of soluble complex l,
Pi ................... the free ion of M,
PjT ................... [Pj] + Σl [Ql],
{[Pn]} ................... set of environmental parameters on which σk and σl depend,
Ql ................... any complex containing M,
R ................... retardation factor = 1 + ρ/n Kd (or 1 + Kd when Kd is dimensionless) (R is dimensionless),
r ................... remobilizable fraction of contaminant M in soil matrix,
ρ ................... bulk density of soil (1.8 kg of soil/L of soil volume),
S(0) ................... the specific activity of an element at reactor shut-down (i.e., the activity of the element per weight of the element consisting of stable and radioactive isotopes, Ci/g),
S(t) ................... S(0) exp(-tln2/T),
σ ................... the thermal neutron capture cross section for the activation of the waste radionuclide from the mother isotope (barn),
Σk ................... the operator Σ meaning summation over k,
T................... radionuclide half life (yr),
v ................... velocity of water front in soil (m/yr),
v' ................... v/R = velocity of contaminant front in soil (m/yr),
[ ] ................... designates the concentration (mol/L),
Appendix A
Parameters Determining Equilibrium Partitioning of Trace Contaminants (References in Parentheses)
Physical/Mineralogical Background Parameters: Adsorbent.
- Composition and mineralogy of soil/rock and of its alteration (weathering) products:
- adsorbent: goethite,
- number of adsorbing sites per unit area of goethite: 10-3 moles/m2 (13),
- fraction of soil particle surface covered by goethite: 0.2,
- surface of soil particle per unit weight of particle: 1 m2 /g,
- density of soil particie (grain): 2.6 g/cm,
- porosity of soil: 0.3.
- Specific surface area of adsorbing phase: goethite: 50 m2 per gram of mineral (7).
- Cation or anion exchange capacity: is calculated by adsorption model.
- Electrostatic properties of surface/water interface: expressed by integral capacitance densities for the innermost layers of the Triple Layer Model (see (14)): C1 = 110 microF/cm2 , C2 = 20 microF/cm2 (12).
Chemical Background Parameters:
Reactions |
| 1. adsorption of major ions |
log K |
Ref. |
| XOH + H+ = XOH2+ |
4.20 |
(12) |
| XO- + H+ = XOH |
10.50 |
(12) |
| XOH + Na+ = XO-Na + H+ |
-9.60 |
(15) |
| XOH + Ca2+ = XO-Ca+ + H+ |
-5.00 |
(16) |
| XOH + Ca2+ + H2O = XO-CaOH + 2 H+ |
-14.50 |
(16) |
| XOH + Cl- + H+ = XOH2-Cl |
5.50 |
(15) |
| XOH + SO42+ + H+ + XOH2-SO4- |
9.10 |
(16) |
| XOH + SO42- + 2 H+ = XOH3-SO4 |
14.40 |
(16) |
| 2. electrochemical potential: oxidizing environment |
| 3. solubility product |
| Ca2+ + CO32- = CaCO3 (calcite) |
8.48 |
(18) |
| 4. complex formation
|
| Ca2+ + CO32- = CaCO3 |
3.22 |
(19) |
| Ca2+ + CO32- + H+ = CaHCO3+ |
11.43 |
(19) |
| Ca2+ + CO32- + 2 H+ = CaH2CO32+ |
2.31 |
(19) |
| Ca2+ + SO42- = CaSO4 |
-12.85 |
(19) |
| Ca2+ + H2O = CaOH+ + H+ |
1.27 |
(19) |
| Na+ + CO32- = NaCO3- |
10.08 |
(19) |
| Na+ + SO42- = NaSO4- |
0.7 |
(19) |
| CO32- + H+ = HCO3- |
10.32 |
(19) |
| CO32- + 2 H+ = H2CO3 |
16.67 |
(19) |
| SO42- + H+ = HSO4- |
1.99 |
(19) |
| Ca2+ + EDTA = CaEDTA |
10.69 |
(20) |
| Ca2+ + H+ + EDTA = CaHEDTA |
13.44 |
(20) |
| EDTA + H+ = HEDTA |
10.26 |
(20) |
| EDTA + 2 H+ = H2EDTA |
16.40 |
(20) |
| EDTA + 3 H+ = H3EDTA |
19.06 |
(20) |
| EDTA + 4 H+ = H4EDTA |
21.06 |
(20) |
|
Nuclide Properties |
| 1. adsorption reaction equilibrium
|
| XOH + Ni2+ + H2O = XO-NiOH+ + H+ |
-10.0 |
(17) |
| 2. complex formation |
| Ni2+ + SO42- = NiSO4 |
2.29 |
(21) |
| Ni2+ + 2 SO42- = Ni(SO4)22- |
1.02 |
(22) |
| Ni2+ + H+ + SO42- = NiHSO4+ |
5.00 |
(23) |
| Ni2+ + Cl- = NiCl+ |
0.00 |
(23) |
| Ni2+ + 2 Cl- = NiCl2 |
0.96 |
(22) |
| Ni2+ + EDTA = NiEDTA |
18.62 |
(23) |
| Ni2+ + H+ + EDTA = NiHEDTA |
13.46 |
(23) |
| Ni2+ + H2O + EDTA = NiOHEDTA + H+ |
6.42 |
(23) |
| Ni2+ + H2O = NiOH+ + H+ |
-9.86 |
(24) |
| Ni2+ + 2 H2O = Ni(OH)2 + 2 H+ |
-19.00 |
(24) |
| Ni2+ + 3 H2O = Ni(OH)3- + 3 H+ |
-30.00 |
(24) |
Chemical Background Parameters:
Pore Water Compositions |
(log of) concentrations of major ions
and trace organic complexing agents |
| Ca2+ |
Na+ |
CO32- |
Cl- |
SO42- |
| -6 |
-6 |
-6 |
-6 |
-6 |
| -6 |
-2 |
-6 |
-6 |
-2 |
| saturation with calcite |
-6 |
saturation with calcite |
-6 |
-2 |
-2
EDTA: 0
EDTA : -7 |
-3
EDTA: 0
EDTA : -7 |
-5
EDTA: 0
EDTA : -7 |
-2
EDTA: 0
EDTA : -7 |
-6
EDTA: 0
EDTA : -7 |
| -4 |
-2 |
-6 |
-2 |
-3 |
Appendix B
Concentrations of nickel in various phases and soils
| Number in Fig. 6, 7 |
Adsorbent (Reference) |
Concentration
(mg/kg) |
| 1 |
kaolinite (43) a |
40 ... 220 |
| 2 |
illite (43) a |
50 ...590 |
| 3 |
chlorite (43) a |
300 ... 740 |
| 4 |
montmorillonite (43) a |
1200 ... 1800 |
| 5 |
freshly precipitated iron hydroxide (43) a |
150 ... 370 |
| 6 |
amorphous silicic acid (43) a |
160 ... 500 |
| 7 |
humic acids (44) a |
2500 ... 8700 |
| 8 |
hydrous iron or manganese oxides (13) a |
600 |
| 9 |
carbonates (45) c |
0.4 |
| 10 |
phosphates (46) c |
0.002 ... 0.3 |
| 11 |
laterites (lower silicate zone on ultramafic rock (47) |
10 000 |
| 12 |
unweathered ultramafic rock (47) |
2000 |
| 13 |
podzol over ultramafic rock in S.E. U.S (48) |
1000 |
| 14 |
sewage sludge (England) (49) |
20 ... 5300 |
| 15 |
sewages sludge (Michigan, U.S.) (50) |
50 ... 3000 |
| 16 |
sediments, baltic sea estuary (51) |
900 |
| 17 |
sediments, north sea estuary (52) |
100 |
| 18 |
sediments, lower Rhine river (46) |
40 |
| 19 |
common soils (35) |
5 ... 500 |
| 20 |
roll front in Wyoming clay (27) |
20 |
Legend:
a: based on cation exchange capacity (CEC) as reported in (43), (44).
Concentration Cs of nickel is Cs = 0.5 CEC p M
where
p = 50 g exchange ohase per kg of soil,
M = molar weight of Ni,
0.5 converts equivalents to moles.
b: based on maximum adsorption capacity C of Fe(OH)3(am): C = m s p
where
m = 1.6 10-5 mol/m2, number of adsorbing sites per unit area of Fe(OH)3
s = 200 m2/g, specific surface area of Fe(OH)3
p = 3 g/kg, weight of Fe(OH)3 coatings on soil,
c: nickel concentation is C p, where C is the concentration of nickel per unit weight of carbonate or phosphate.
C = 30 mg Ni per kg of carbonate material (45),
C = 8 ... 70 mg Ni per kg of phosphate material (46),
p = 20 g carbonates per kg of soil (35),
p = 0.2 ... 5 g phosphate material per kg of soil (35).
Environments 11 - 13 included to show change of nickel content due to wheathering.
Environment 20: value gives increase of nickel concentration due to nickel roll front.
Version: October 20, 2018
Address (URL) of this paper
Physics Home
Joachim Gruber






