Concentration Waves: Chromatographic Theory and Experimental Verification

Joachim Gruber
E-Mail: Joachim_Gruber
Address at the time this paper was finished:
Arbeitsbereich Umweltschutztechnik, Technische Universität,
Eissendorfer Str. 40, D 21073 Hamburg, Germany

ABSTRACT

Aqueous transport of negative ions (OAc^-, Cl^-, OH^-) in a column filled with a positively charged ion exchange resin is described with a quasilinear set of hyperbolic conservation laws (mass balance equations). Analytical solutions of the Riemann problem (a single abrupt change of the ion concentrations at the column input) are found and discussed for the exact and asymptotic systems. An experiment performed 1984 by Barbara J. Bennett is interpreted with the presented formalism.

Introduction

There are two major research areas in the field of ion transport in aqueous porous media:

the movement of the water, sometimes simplified as advective - dispersive flow [Oelkers, 1996],
the influence of chemical reactions among the ions and between them and the porous medium (exposed to the ions) in the flow channels [Stumm and Morgan, 1981].

This paper will address the second area, assuming thermodynamic equilibrium in the flow channels. The mass action laws describing the chemical reactions are generally non-linear.

The chemical composition of the liquid or solid phases (speciation) in spatially homogenous (so called batch) systems change qualitatively when concentrations move through certain boundaries (thresholds) given by the mass action law constants describing the chemical interactions [see e.g. page 65, Morel and Hering, 1993]. The reason for this is the non-linearity introduced by the mass action laws. It is virtually impossible to predict the chemical composition on the other side of a concentration threshold when experimental or numerical results are available only on this side of the threshold and thus even the existence of the threshold is unknown. It's like walking around the edge of a building: You simply cannot know ahead of time what you will be facing behind the building.

After non-linear geochemistry has been added to transport models, the same became true for the resulting models. The Conclusions section will summarize the manifestations of non-linear processes in the simple exchange system presented here. This will exemplify, that

like analytical speciation models allow us to make a guess as to where concentration thresholds might be,
similarly, chromatographic models allow predictions and interpretations of transport processes

by giving us access to the governing equations, i.e. the speciation laws and the hyperbolic conservation laws, respectively.

Finally, I will show to what extent the presented chromatographic solutions of the transport problem coincide with the observed concentration waves.

General Properties of Multicomponent Chromatography

The following theorems are basic to the theory of multicomponent chromatography and will be stated without proof (see Gruber, 1990, 1995, 1996 for a general introduction into the solutions of hyperbolic conservation laws using a notation consistent with the one in this paper).

Definition:
Riemann problem and centered rarefaction waves

The set of conservation laws will be solved for a single abrupt change (Riemann jump) of the chemical composition of the feed water (Riemann problem):

c(x ≤ 0, t=0) = c_- (feed water composition),
c(x>0, t=0) = c₊ (pre-equilibrant water composition).

The solution considered here is the centered k-rarefaction wave, because from a practical point of view this class of solutions will comprise also the shocks, the other relevant class of solutions. The sequence of k-waves c(x = l, t) is called breakthrough curve.

In a centered k-rarefaction wave

the concentration c(x, t) varies continuously and usually non-periodic with ξ = x/t,
the spatial or temporal distance between the characteristics increases with increasing x or t,
of a set generally non-uniquely defined properties of the system (Riemann invariants), w_j (j = 1, 2, ..., n₀), the k-Riemann invariant w_k changes while the other w's remains constant. In this sense the k-wave is the propagation of property w_k along the column.

Theorem:
Riemann invariants

Properties and physical meaning of the Riemann invariant:

When all Riemann invariants are known, all waves can be calculated.
Often, one can guess some Riemann invariants from the physico-chemical properties of the system. For example, in the 2-component system discussed below, w₁ = [OAc], w₂ = [Na⁺] (with boldface symbols referring to adsorbed species, see Notation section). Another choice of Riemann invariants would be w₁ = [OH], w₂ = [Na⁺].
Only when there are no chemical interactions, the choice of the w_k is obvious: the Riemann invariants are the concentrations of the chemical components. Therefore, a common mistake in interpreting numerically computed transport profiles is to identify the observed waves with the components instead of the Riemann invariants.

Theorem:
Grid of shocks and rarefaction-waves

When the separation factors are independent from the concentrations (as in (4)) and complex formation in water is negligible,

k-rarefaction waves are (straight) lines in concentration space,
shocks and rarefaction waves coincide, and
the waves are invariant manifolds, meaning that the waves can be assembled into a grid of lines that is a function only of the chemical interactions, i.e. not dependent on the Riemann jump.

2-Component System: Na - OAc - OH

In the first example an aqueous solution of only sodium acetate migrates through the ion exchange column (for meaning of the symbols that follow see Notation Section in the back):

Definition 1:
Number of species and constraints

The chemical system consists of 7 species:

Na⁺, (HOAc, OAc^-), (H⁺, OH^-), OAc^-, OH^-.................... (1)

where underlined species are bound to X_T permanent positive charges on an ion exchange surface.
The concentrations of species in parentheses are correlated by solution mass action equilibria:

[HOAc] = β [OAc^-] [H⁺], β = 10^4.75 L of water/mol.................... (2)
[H⁺] [OH^-] = K_w = 10^-14 (mol/L of water)².................... (3)
Adsorbed fractions are related by the separation factor α

[OAc] [OH^-] / ([OAc^-] [OH]) = α_OAcOH = 2.96.................... (4)
Electroneutrality is required for the aqueous and adsorbed phases:

[Na⁺] = [OAc^-] + [OH^-] - [H⁺].................... (5)
X_T = [OAc] + [OH] = 1.2 mol/L of system volume (ion exchange bed).................... (6)

Definition 2:
Components and conservation laws

The number n₀ of independent species ("components") is

n₀ = n_s - n_c = 2

where n_s is the number of species (n_s= 7) and n_c the number of constraints (n_c = 5).
We can choose any two conserved species as components. Species are conserved when they are neither created nor destroyed in the waves. Conserved species are sodium (Na⁺), acetate (Ac)

[Ac] = [OAc^-] + [HOAc] = [OAc^-] (1 + β K_w/[OH^-].................... (7)

and hydroxyl-surplus (hydroxyl ions count positive, any ion that can destroy a hydroxyl counts negative)

hydroxyl surplus = [OH^-] - [H⁺] - [HOAc]..................... (8)
The hyperbolic conservation laws for acetate, sodium and hydroxyl-surplus are [Gruber, 1990]

(v_w/φ - ξ)([OAc^-] + [HOAc])'- ξ/φ [OAc]' = 0.................... (9)

(v_w/φ - ξ)[Na⁺]' = 0 .................... (10)

(v_w/φ - ξ)([OH^-] - [H⁺] - [HOAc])' - ξ/φ [OH]' = 0.................... (11)

All sets of any two of these conservation laws are mathematically equivalent. We will choose
- OAc^- and OH^- as components,
- as "concentration space" the space with [OAc^-] as abscissa and [OH^-] as ordinate,
- from the conservation laws the ones that will provide us with the most compact interpretation.

Theorem 1:
Waves in the Na - OAc - OH system

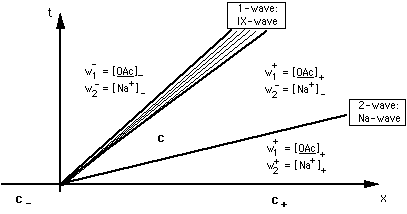
Solution of Riemann problem for Na-OAc-OH system

FIGURE 1: Solution of the Riemann problem for Na-OH-OAc system. Lines ("characteristics") are location of arbitrarily selected concentrations c(ξ) within the waves. Waves are bounded by heavy lines, the concentrations of the constant states. Constant state vectors are c_- = {[OAc^-]_-, [OH^-]_-}, c = {[OAc^-], [OH^-]}, c₊ = {[OAc^-]₊, [OH^-]₊}. ξ = x/t is the slope of the characteristic for c(ξ). Constant state concentrations in fan of waves are given for the Riemann invariants, [Na⁺] = [OAc^-] + [OH^-] - [H⁺] and [OAc]. 2-wave is non-retarded.

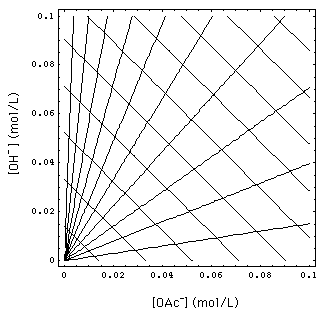
Waves in concentration space for Na-OAc-OH system

Waves in concentration space for Na-OAc-OH system

FIGURE 2. Waves in concentration space. 1-waves are the ones that are parallel and have a slope -1. 2-waves form the fan originating from the coordinate origin. They are (straight) lines because of 1/1 exchange process. [Na⁺]_- = 0.02, 0.04, ..., 0.2 mol/L. Abscissa: concentration of OAc in solution, ordinate: concentration of OH in solution.

The set (9) and (11) of conservation laws has two spatially continuous solutions, the 1- and the 2-rarefaction wave. Fig. 1 gives a schematic of the waves and Riemann invariants in physical {x, t} space. Fig. 2 shows some 1- and 2-waves in concentration space.

The 1-rarefaction wave ("ion exchange wave")

It is retarded, ξ ≠ v_w/φ (= speed of the water).
It is the propagation of the jump in adsorber composition w₁ along the column.
Across this wave
- w₁ = [OAc] or [OH] (the speciation on the adsorber) changes from [OAc]_- or [OH]_- to [OAc]₊ or [OH]₊,whereas
- w₂ = [Na⁺] remains constant.
- From the invariance of the Riemann invariant w₂ we can derive the implicit equation of the 1-wave in concentration space:
  [Na⁺] = [OAc^-] + [OH^-] - [H⁺] = [OAc^-]_- + [OH^-]_- - [H⁺]_- = [Na⁺]_-. (explicit form)
In concentration space it is a line with slope -1 at [OH^-] >> [H⁺]. The reason for this slope is the 1/1 adsorption stoichiometry specified in the separation factor (4) and adsorber electroneutrality (6): one OAc^- ion is exchanged for one OH^- ion (more on this in the appendix).

The 2-wave ("sodium wave")

It is non-retarded, ξ = v_w/φ ("indifferent wave").
It is the propagation of the jump in sodium concentration w₂ along the column.
Across this wave
- w₂ = [Na⁺] changes from [Na⁺]_- to [Na⁺]₊, whereas
- the speciation on the adsorbing surface remains constant.
- From the invariance of Riemann invariant w₁ we can derive the equation of the 2-wave in concentration space:
  [OAc^-] = [OAc^-]₊ [OH^-]/[OH^-]₊.
The 1/1 adsorption stoichiometry is the reason for the waves to be (straight) lines in concentration space (more on this in the appendix).

Proof

Notation for proof:

Let

superscripts + and - on the Riemann invariants and

subscripts + and - on the concentrations

denote the constant states + and - upstream and downstream of the 1- and 2-wave, respectively, i.e. let the superscripts on w_j specify the state at which the Riemann invariant is evaluated:

w₁^- = [OAc]_-, w₁⁺ = [OAc]₊,.................... (12)

or w₁^- = [OH]_-, w₁⁺ = [OH]₊, .................... (12')

and w₂^- = [Na⁺]_-, w₂⁺ = [Na⁺]₊..................... (13)

Similarly, let

α⁺_OAcOH = [OAc]₊[OH^-]₊/([OAc^-]₊[OH]₊) .................... (14)

be the separation factor evaluated at c₊.

Let a concentration without index be the concentration

on the 1-wave in the proof for the 1-wave
on the 2-wave in the proof for the 2-wave.

We choose as Riemann invariants

w₁ = [OAc], .................... (15)

or w₁ = [OH], .................... (15')

and w₂ = [Na⁺]..................... (16)

This choice is based on the following argument: According to (10), one solution, the 1-wave, has the properties

ξ ≠ v_w/φ and [Na⁺]' = 0.................... (17)

i.e. the wave is retarded, and propagates the surface composition jump, as [OAc] and [OH] change ([OAc]' ≠ 0 ≠ [OH]'). The other solution of (10) is

ξ = v_w/φ and [OAc]' = [OH]' = 0. ....................(18)

Fig. 1 gives the values of the Riemann invariants in the fan of waves. From this pattern of Riemann invariants we will derive the equations of the waves.

1-Wave

The invariance (12) of w₂ across the 1-wave together with the electroneutrality in water, (5), tells us

[Na⁺]_-= [OAc^-] + [OH^-] - [H⁺].................... (19)

We can use the H⁺/OH^- equilibrium, (3), to eliminate [H⁺] from (19), solve for [OH^-] and get the representations of the 1-wave:

[OH^-] = a + √[a² + K_w] ..........(1-wave).................... (20)

where a = 1/2 ([Na⁺]_- - [OAc^-]) and √ stands for the square root. At pH > 7 the 1-wave (19) is approximately a line with slope -1:

[OH^-] = [Na⁺]_- - [OAc^-] (for [OH^-] >> [H⁺])..................... (20')

Note that this slope reflects the 1/1 OAc^-/OH^- exchange process.

2-Wave

The other solution of (10) is

w₂' = [Na⁺]' ≠ 0 and ξ = v_w/φ ..................... (21)

The 1-Riemann invariant is constant:

w₁ = w₁⁺

or using the expression for w₁

[OAc] = [OAc]₊ and [OH] = [OH]₊.................... (22)

Then due to the invariance of w₁,

α⁺_OAcOH = [OAc][OH^-]₊/([OAc^-]₊[OH^-])..................... (14')

By assumption the separation factor is independent from the concentrations:

α⁺_OAcOH = α_OAcOH = 2.96.................... (23)

Solving this relationship for [OH^-] gives us the equation of the 2-wave

[OH^-] = [OH^-]₊ [OAc^-]/[OAc^-]₊..........(2-wave)..................... (24)

Note that some other than the 1/1 exchange stoichiometry would show up in a separation factor involving higher powers of the concentration ratios. This non-linearity would then be passed on to the shape of the non-retarded wave.

Corollary

The neutral complex HOAc is without influence on the representation of the waves in concentration space (it does affect the retardation of the 1-wave).

Proof: [HOAc] did not enter into the deductions of the 1- and 2-wave equations.

3-Component System: Na - OAc - Cl - OH

When Cl^- ions are added to the water of the previous system, we obtain 2 more variables, [Cl^-] and [Cl], and one more constraint (25). Therefore the system has 3 components, now:

Definition 4:
Number of species and constraints

The chemical system consists of 9 species:

Na⁺, (HOAc, OAc^-), (H⁺, OH^-), Cl^-, OAc^-, OH^-, Cl^-
The two solution equilibria are the same as in the Na-OH-Ac system, i.e. (2) and (3).
The separation factors are

[OAc] [OH^-] / ([OAc^-] [OH]) = α_OAcOH = 2.96.................... (4)

[Cl] [OH^-] / ([Cl^-] [OH]) = α_ClOH = 7.39.................... (25)
The electroneutrality conditions are

[Na⁺] = [OAc^-] + [Cl^-] + [OH^-] - [H⁺].................... (26)

X_T = [OAc] + [Cl] + [OH] = 1.2 mol/L of system volume (ion exchange bed).................... (27)

Definition 5:
Components and conservation laws

The number of components is 3 (9 variables - 6 constraints). As components we choose OAc, hydroxyl surplus and chloride.
The set of conservation laws consists of the corresponding two equations from the Na-OAc-OH system augmented by the equation for chloride. We choose

(v_w/φ - ξ)([OAc^-] + [HOAc])'- ξ/φ [OAc]' = 0.................... (9)

(v_w/φ - ξ)([OH^-] - [H⁺] - [HOAc])' - ξ/φ [OH]' = 0.................... (11)

(v_w/φ - ξ)[Cl^-]' - ξ/φ [Cl]' = 0 .................... (28)

Theorem 3:
Waves

The addition of chloride ions introduces one more retarded wave. What has been said in Theorem 1 about the retarded wave can be generalized here to the two retarded waves. The 3-wave here is the analog of the 2-wave characterized in Theorem 1:

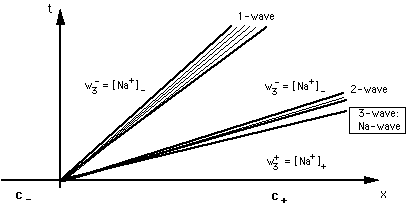
FIGURE 3 : Fan of waves in 3-component system Na-OAc-Cl-OH. c_-= {[OAc^-]-, [Cl^-]-, [Na⁺]-}, c₊= {[OAc^-]₊, [Cl^-]₊, [Na⁺]₊}. Across the non-retarded (3-)wave concentration of sodium changes from [Na⁺]₊ to [Na⁺]_-. Concentration vectors on the 3- or 2-wave will be referred to as c = {[OAc^-], [Cl^-], [Na⁺]}.

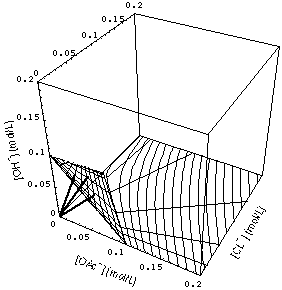
Waves in concentration space of Na-OAc-Cl-OH system

Waves in concentration space of Na-OAc-Cl-OH system

FIGURE 4. Some 3-waves (eq. (33), heavy lines) and surface (36) for [Na⁺]_- = 0.1 mol/L with 1- and 2-waves. Asymptotic equations (42), (44) and (51), (52) used for 1-, 2-waves, respectively. 2-waves is the starlike fan of lines.

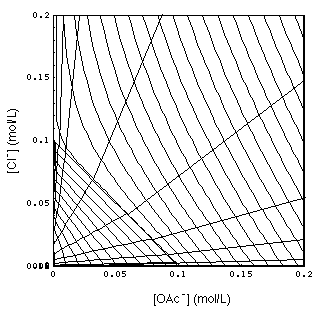
Projection of 1- and 2-waves of Fig. 4 onto OAc-Cl plane

Projection of 1- and 2-waves of Fig. 4 onto OAc-Cl plane

FIGURE 5. Same as Fig. 4 (with 3-waves omitted), view is perpendicular onto {[OAc^-], [Cl^-]} plane. 1-waves are more densely spaced lines with negative slope. Their upward bending is a consequence of the HOAc complex. Waves exist on the right side of the line intersecting the axes at 0.1 mol/L because of the water dissociation, the H⁺/OH^- equilibrium.

The 1-and 2-rarefaction waves ("ion exchange waves")

are the propagation of the jump in adsorber composition along the column.

Across these two waves [OAc] and [OH] change from [OAc]_- and [OH]_- to [OAc]₊ and [OH]₊ while w₂ = [Na⁺] remains constant. From the invariance of the Riemann invariant w₂ across these waves we can derive the equation of the plain in which the 1- and 2-waves lie:
[Na⁺] = [OAc^-] + [Cl^-] + [OH^-] - [H⁺] = [OAc^-]_- + [Cl^-]_- + [OH^-]_- - [H⁺]_- = [Na⁺]_-
This surface is bent near the line [OAc] + [Cl] = const.
are retarded, ξ ≠ v_w/φ.
can be asymptotically represented (click here if you do not want to see explicit asymptotic equations of waves)
- at low pH as
  1-waves:
  
  [Cl] = (β[Na⁺]_-/b - 1)[OAc^-] + (b*_-[OAc]_- + [Cl]_-) / b....................( 43)
  
  with
  
  b = 1 + β[OAc^-], b_-* = 1 + β K_w/[OH^-]_-
  
  [OH^-]_- = a_- + √[a_-2 + K_w].................... (20)
  
  a_- = ([Na⁺]_- - [OAc^-]_- - [Cl^-]_-)/2
  2-waves:
  [OAc] = [OAc^-]₊/[Cl^-]₊ [Cl^-].................... (44)
- at high pH as
  1-waves:
  
  [Cl^-] = Cl^u_p + dCl^u_p/d[OAc_p] ([OAc^-] - [OAc_p]) .................... (51)
  
  2-waves:
  
  [Cl^-] = Cl^l_p + dCl^l_p/d[OAc_p] ([OAc^-] - [OAc_p]).................... (52)
  
  The parabola Cl^{l, u}_p and its tangents are shown in Fig. 7.

The 3-wave ("sodium wave")

is the propagation of the jump in sodium concentration w₃ along the column. Across this wave w₃ = [Na⁺] changes from [Na⁺]_- to [Na⁺]₊, whereas the speciation on the adsorbing surface remains constant. Across the 3-wave the speciation on the adsorber is invariant. From that property we can derive the equation of the 3-wave:
[OAc^-] = [OAc^-]₊ [OH^-]/[OH^-]₊,
[Cl^-] = [Cl^-]₊ [OAc^-]/[OAc^-]₊
is non-retarded, ξ = v_w/φ ("indifferent wave").

Click here to jump over proof of this theorem.

Proof

The sum of the set of conservation laws (9), (11), (28) is

(v_w/φ - ξ)([OAc^-] + [Cl^-] + [OH^-] - [H⁺])' - ξ/φ ([OAc] + [Cl] + [OH])'= 0
........(29)

Electroneutrality on the surface (27) requires that the sum of all adsorbed concentrations equaling the ion exchange capacity X_T be constant. Thus ([OAc] + [Cl] + [OH])' = 0. Therefore (29) is simply

(v_w/φ - ξ)([OAc^-] + [Cl^-] + [OH^-] - [H⁺])' = 0 .................... (29')

which is the conservation law for Na⁺(see electroneutrality condition (26)). We will choose

w₃ = [Na⁺]..................... (30)

Na⁺ is a component we could have chosen instead of one of the others, OAc and Cl.

3-wave

The proof of point 2 of the theorem on the 3-wave is analogous to the corresponding proof in the chloride free system. Let c = {[OAc^-], [Cl^-], [OH^-]} lie on the 3-wave (see Fig. 3). Across a non-retarded wave, ξ = v_w/φ, the concentrations on the surface cannot change (see conservation laws (9, 11, 28):

[OAc]' = 0, or [OAc] = [OAc]₊.................... (31)
[Cl]' = 0, or [Cl] = [Cl]₊
[OH]' = 0, or [OH] = [OH]₊

The equation for the 3-wave in three-dimensional concentration space c = {[OAc^-], [Cl^-], [Na⁺]} is given by the invariance of the separation factors

α⁺_OAcOH= α_OAcOH.................... (32)
α⁺_ClOH = α_ClOH

where the separation factors are evaluated at the compositions c⁺ and c, downstream and upstream of the 3-wave, respectively. Using the invariance relations (30) in (31) gives us the equations for the 3-wave:

[OH^-] = [OH^-]₊/[OAc^-]₊ [OAc^-].................... (33)

[Cl^-] = [Cl^-]₊/[OAc^-]₊ [OAc^-].

Note that like in the 2 component system separation factors that are non-linear in the ratios of the concentrations would pass this non-linearity on to the shape of the waves.

1- and 2-rarefaction wave

The 1- and 2-waves have to meet the condition (29') for non redarded speeds ξ: v_w/φ ≠ ξ:

[Na⁺] = [OAc^-] + [Cl^-] + [OH^-] - [H⁺] = [Na⁺]_- ,.................... (34)

Again, like in the OAc - OH system above, the water dissociation equilibrium (3) is used to eliminate [H⁺],

[OAc^-] + [OH^-] + [Cl^-] - K_w/[OH^-] = [Na⁺]_-, ....................(35)

and the resulting expression is solved for [OH^-],

[OH^-] = a + √[a² + K_w].................... (36)

with

a = ([Na⁺]_- - [OAc^-] - [Cl^-])/2

Fig. 4 shows the surface (36) in concentration space. It can be envisaged as a surface attached to and having a bend near the line [OAc^-] + [Cl^-] = [Na⁺]_- in the {[OAc^-],[ Cl^-]} plane.

Since the exact Riemann invariants for the subsystem with constant [Na⁺] cannot be guessed from physico-chemical principles, I will calculate the 1- and 2-waves in two ways:

from the eigenvectors of the Jacobian of the adsorption isotherms.
Pro: This method is fast and reliable. The results are displayed in Figs. 4 and 5.
Con: Leaving the computer handle the eigenvalue problem gives us little insight into the physico-chemistry behind the resulting wave forms.
by directly solving a set of approximated conservation laws like in the 2-component Na-OAc-OH system since
- either the Riemann invariants can be guessed or
- analytical solutions of the conservation laws can be obtained.
  Pro: We will see that the system has two asymptotical solutions that can be readily joined. The asymptotic systems are well known 2-component systems.
  Con: The analytical solution of the set of conservation laws is somewhat lengthy to derive. It will be found in [Gruber, 1996].

Eigenvectors of the Jacobian

The adsorption isotherms C_i = [OAc], [Cl] and [OH] can be constructed combining the definitions (4), (25) of the separation factors and of the ion exchange capacity (27):

C_i([OAc^-], [Cl^-], [OH^-]) = X_T a_{i OH} c_i / d.................... (37)

with

d = α_OAcOH[OAc^-] + α_ClOH[Cl^-] + [OH^-]

where c_j = [OAc^-], [Cl^-] or [OH^-].

The elements of the Jacobian matrix C'([OAc^-], [Cl^-], [OH^-]) of the isotherms are the partial derivatives of the isotherms with respect to the concentrations [OAc^-], [Cl^-] and [OH^-] [Gruber, 1990]. The k-waves c_k are everywhere tangential to the k-eigenvectors r_k of this matrix C'. I have constructed the k-waves from the k-eigenvectors with a suitable Euler or Runge-Kutta method [Gruber, 1995].

As long as the waves are (straight) lines (which is predominantly the case in the systems discussed here), the fastest and most convenient integration procedure is the Euler method. The k-wave is composed of segments

c_k(n) = c_k(n-1) + Delta r_k(c_k(n-1)).................... (38)

where n is the segment number and Delta is the length of a segment pointing in the direction of the k-eigenvector r_k(c_k(n-1)) evaluated at the beginning of the wave segment c_k(n-1).

Asymptotic Solution 1: Low pH Approximation of 1- and 2-Waves:
(Negligible Adsorption of OH^-)

If the adsorbed OH^- ions can be neglected, i.e. if

[OAc] + [Cl] >> [OH].................... (39)

which is equivalent to

α_OAcOH[OAc^-] + α_ClOH[Cl^-] >> [OH^-],.................... (39')

the conservation law for [OH^-] can be dropped from the set (9), (11), (28). The remaining set describes exchange between acetate and chloride, which can be solved similarly as the exchange between acetate and hydroxyl in the Na-OAc-OH system:

(v_w/φ - ξ) ([OAc^-] {1 + β [H⁺]})' - ξ/φ [OAc]'= 0 .................... (9)

(v_w/φ - ξ) [Cl^-]' - ξ/φ [Cl]'= 0 .................... (28)

The sum of these conservation laws (abbreviating [Ac] = [OAc] {1 + β [H⁺]})

(v_w/φ - ξ) ([Ac] + [Cl^-])' - ξ/φ ([OAc] + [Cl])'= 0

can be solved, because -for negligible [OH]- OAc and Cl cover the entire ion exchange resin surface ([OAc] + [Cl] = X_T):

(v_w/φ - ξ) ([Ac] + [Cl^-])' = 0,.................... (40)

For ξ ≠ v_w/φ, the 1-wave,

w₁ = ([Ac] + [Cl^-])' = 0.................... (41)

which can be integrated -as above:

[Ac] = [Ac]_- - [Cl^-] + [Cl^-]_-..................... (42)

Plugging electroneutrality in water, (34) with constant [Na⁺] = [Na⁺]_- across the 1- and 2- wave, (see Fig. 3),

[OAc^-] + [Cl^-] - [H⁺] = [Na⁺]-,

(the latter equation includes the low pH approximation (39)).

into (42) and solving for [Cl^-] we arrive at the low pH approximation for the 1-wave

[Cl] = (β[Na⁺]_-/b - 1)[OAc^-] + (b*_-[OAc]_- + [Cl]_-) / b.................... (43)

with

b = 1 + β[OAc^-], b_-* = 1 + β K_w/[OH^-]_-

[OH^-]_- = a_- + √[a² + K_w].................... (36)

a_- = ([Na⁺]_- - [OAc^-]_- - [Cl^-]_-)/2

[OH^-] = f([OAc^-], [Cl^-]) is the surface (36) with the 1- and 2-waves.

The fast (2-)wave in the system (9) and (28) is non-retarded (it is non-retarded only in the framwork of the low pH approximation). It is a line through the point {[OAc^-]₊, [Cl^-]₊} and the origin of concentration space {[OAc^-], [Cl^-]} = {0, 0}.

[OAc] = [OAc^-]₊/[Cl^-]₊ [Cl^-].................... (44)

The proof is analogous to the one given for the 2-component system.

(43) and (44) are the waves in the low pH region (right part of Fig. 5).

Asymptotic Solution 2: High pH Approximation
(Negligible HOAc complex)

In the high pH approximation the presence of protons i.e. H⁺ and HOAc, is neglected.

[OH^-] >> [H⁺] - [HOAc].................... (45)
[OAc^-] >> [HOAc]..................... (46)

Thus, the set of conservation laws (9), (11) and (28) assumes the following simple form

(v_w/φ - ξ)[OAc^-]'- ξ/φ [OAc]' = 0.................... (9')

(v_w/φ - ξ)[OH^-]' - ξ/φ [OH]' = 0 ....................(11')

(v_w/φ - ξ)[Cl^-]' - ξ/φ [Cl]' = 0 .................... (28)

We get a Langmuir type adsorption isotherm due to

the truncated electroneutrality in water

[OAc^-] + [Cl^-] + [OH^-] = [Na⁺]_-,.................... (35')
the definitions (4) and (25) of the separation factors and
the definition (27) of the capacity of the ion exchange resin

of the form

C_i([OAc^-], [Cl^-], [OH^-]) = X_T a_i OH c_i / dl.................... (47)

with

dl = 1 + (α_OAcOH - 1)[OAc^-] + (α_ClOH - 1)[Cl^-],

c_i = c_i/[Na⁺]_-.

The analytical solution of this type of equations (9'), (11'), (28) and (35') has been published in the literature [Rhee, Aris, Amundson, 1989] and been applied to the present set of equations by Gruber [1996].

The solution of this 2-component system are waves that lie on lines tangential to a parabola (see Fig. 6)

Cl^l_p = k - [OAc_p]/k + 2 √[-[OAc_p]/k] (lower branch of parabola).................... (48)

Cl^u_p = k -[OAc_p]/k - 2 √[-[OAc_p]/k] (upper branch of parabola).................... (49)

where

k = - (1 - aOAcCl)/(1 - α_OAcOH) [Na⁺]_-..................... (50)

The equations of the 1-waves are

[Cl^-] = Cl^u_p + dCl^u_p/d[OAc_p] ([OAc^-] - [OAc_p]) .................... (51)

and of the 2-waves

[Cl^-] = Cl^l_p + dCl^l_p/d[OAc_p] ([OAc^-] - [OAc_p]).................... (52)

The waves (tangents to the parabola) are shown in Fig. 6.

Physical interpretation of the grid of 1- and 2-waves: Buffers

For the following discussion, note that the parabola touches the concentration axes at [OAc^-] = - k and [OH^-] = k .

High pH approximation: conservation laws (9'), (11'), (28).
In the simple 2-component system above with ion exchange of type (37) (with all Cl^- terms dropped) one OAc^- replaces one [OH^-] (or vice versa) on the adsorbing surface. In the high pH approximation Langmuir type 2-component system (47) a third ion (here OH^-) acts as buffer, thus relaxing the strict one to one replacement typical for the simple 2-component system. This leads to the difference in the wave patterns between Fig. 2 and Fig. 5. Adsorption of OH^- disengages the 2-waves from the origin and steepens the 1-waves. The stronger the OH^- ions bind to the surface or, formally, the more the separation factor α_OAcOH approaches unity and the more k increases therewith, and the more pronounced become these features.
Low pH approximation: conservation laws (9) and (28).
Continue the grid of low pH waves (right part of Fig. 5 into the high pH region (inside the triangle bounded by the line [OAc^-] + [Cl^-] = [Na⁺]_- = 0.1 mol/L. The deviation of this extrapolated grid from the grid actually drawn in the triangle of Fig. 5 is the error of the low pH approximation. Thus, the reduced set of conservation laws of the low pH approximation suffices as long as k (and therfore the extension of the parabola) is small (k < [OAc^-] + [Cl^-]).

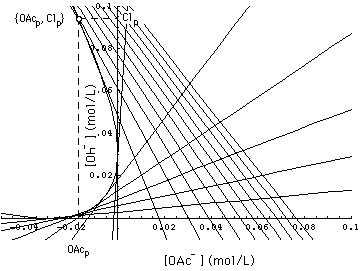
Parabola and 1- and 2-waves in Na-OAc-Cl-OH system

FIGURE 6. Parabola (48), (49) and calculated asymptotic 1- and 2-waves (51), (52), in a 2-component system with conservation laws (9'), (11'), (28) and constant normality [Na⁺]_- = 0.1 mol/L, (35'). These high pH asymptotic waves tangential to the parabola and the exact waves (i.e. the waves (38), derived from the Jacobian) coincide in the triangle bounded by the line [OAc^-] + [Cl^-] = [Na⁺]_- = 0.1 mol/L. 1-waves are the lines with negative slope. k = 0.306 [Na⁺]- . a_OAcCl = 0.4, α_OAcOH = 2.95.

Comparison with Experiment

In 1984, Barbara J. Bennett performed experiments with the 2- and 3-component systems discussed here and interpreted the results on the basis of Helfferich's version (the original version) of multicomponent chromatography [Helfferich and Bennett, 1984a, b]. She used the Rohm & Haas Amberlite IRA-400 strong-base anion exchange resin. Chemical equilibrium between adsorber resin and the liquid phase was assumed.

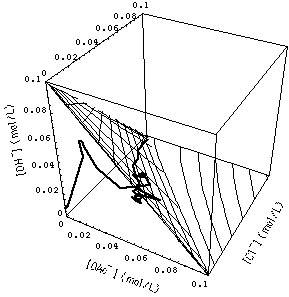
Fig. 7 shows a portion of concentration space with the calculated grid of 1- and 2-waves and the experimentally determined 1-, 2- and 3-waves ("observed composition path"). Since measurement errors were not reported, I am not able to decide whether the observed 3-wave actually stops short of the surface [Na⁺]_- in which the 1- and 2-waves run. If one allows an uncertainty of 0.2 pH units (or less in unison with uncertainties of [OAc^-] and [Cl^-]), the 3-wave runs into the required surface.

Fig. 8 allows a comparison of the observed composition path and the calculated grid of the 1- and 2-waves. Helfferich and Bennett comment that

the random walk appearance of the composition path suggests that part of the deviation between calculated and observed waves should be attributed to lack of accuracy of their acetate analysis.
according to their opinion the main part of the incongruence might be caused by a concentration dependency of the separation factors which has been neglected in this analysis.

Grid of 1- and 2-waves together with experimental composition path in Na-OAc-OH system

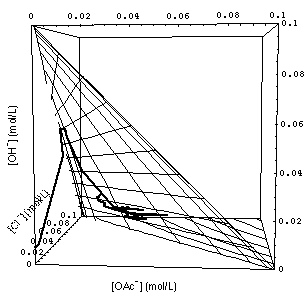
FIGURE 7. Calculated grid of 1- and 2-rarefaction waves (see Fig. 4) and experimentally observed waves (path through concentration space represented by heavy curve). Note that the calculated 3-wave (connecting the origin of concentration space {[OAc^-], [Cl^-], [OH^-]} = {0, 0, 0} with the surface of the 1- and 2-wave grid) has been omiited to avoid clutter. Upper and lower part of the figure differ only in the point from which concentration space is viewed.

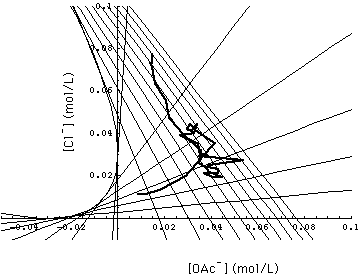
Grid of 1- and 2-waves together with experimental composition path projected onto OAc-Cl plane in Na-OAc-OH system

Grid of 1- and 2-waves together with experimental composition path projected onto OAc-Cl plane in Na-OAc-OH system

FIGURE 8. Experimentally determined 1- and 2-wave (observed composition path, heavy line) entered into Fig. 6. Main part of deviation between observation and multicomponent chromatography as presented in this paper is attributed to concentration dependent separation factors not considered in this analysis [Helfferich and Bennett, 1984a and b].

Conclusions

The grid of k-waves in concentration space is calculated

from the eigenvectors of the Jacobian of the multicomponent adsorption isotherm,
by analytically solving a set of exact or asymptotic hyperbolic (i.e. diffusion/hydrodynamic dispersion free) mass conservation laws.

The grid topology reflects the non-linearity introduced by the chemical interactions and reveals the relevant processes, i.e.

soluble complex formation (curvature of the 1-waves in Fig. 5 at low pH),
water dissociation (in Fig. 5 presence of waves in the region outside the triangle bounded by the line intersecting the axes at 0.1 mol.L),
the stoichiometry of the adsorption reactions and
buffers on the adsorbing surfaces.

When the breakthrough curves c(x = l, t) of the 2- and 3-component ion exchange system are drawn in concentration space, the resulting composition path aligns to a degree with the grid of k-waves that seems satisfactory for environmental assessments.

Acknowledgement

I wish to thank Friedrich G. Helfferich of The Pennsylvania State University, University Park, PA, USA for having encouraged this work and helped me find these experimental data. The data have been generated by Barbara J. Bennett in the framework of her thesis for the Degree of Master of Science in the Department of Chemical Engineering at Penn State University.

Notation

[Ac].......... concentration of acetate (= [OAc^-] + [HOAc]) in water (mol/L of water),
α_ClOH.......... constant (i.e. concentration independent) separation factor (25) (dimensionless),
α_OAcOH.......... constant (i.e. concentration independent) separation factor (4) (dimensionless),
β.......... HOAc complex formation constant (= [HOAc]/[OAc^-]) (dimensionless),
[Cl^-].......... concentration of chloride in water (mol/L of water),
[Cl].......... concentration of chloride on adsorbing surfaces (mol/L of system ("IX bed")),
[Cl_p].......... Cl^- concentration on parabola (mol/L of water),
c.......... concentration vector in water (= {[OAc^-], [Cl^-], [OH^-]}) (mol/L of water),
c_j ..........normalized concentration of component j (= c_j/[Na⁺]_- ) (mol/L of water),
concentration space ..........{[OAc-], [Cl-], [OH-]} space,
d.......... adsorption isotherm denominator (= α_OAcOH[OAc^-] + α_ClOH[Cl^-] + [OH^-], (37)) (mol/L of water),
d_l.......... Langmuir adsorption isotherm denominator (= 1 + α_OAcOH[OAc^-] + α_ClOH[Cl^-], (47)) (dimensionless),
φ (or f).......... fraction of system volume filled with water (0.4),
[H⁺].......... concentration of free protons in water (mol/L of water),
[HOAc].......... concentration of HOAc complex in water (mol/L of water),
K_w.......... dissociation constant of water (mol²/L² of water),
k.......... size parameter of parabola (= - (1 - a_OAcCl)/(1 - α_OAcOH) [Na⁺]_-) (mol/L of water),
k.......... index of k-rarefaction wave. An n₀ component system has n₀ k-rarefaction waves (k = 1, ... n₀),
l.......... length of the ion exchange column (m),
l.......... superscript assigned to quantities referring to lower part of parabola,
[Na⁺].......... concentration of sodium in water (mol/L of water),
[Na⁺]_-.......... concentration of sodium in column feed (mol/L of water),
[Na⁺]₊.......... concentration of sodium in column at t = 0 (pre-equilibrant) (mol/L of water),
n₀.......... number of chemical components and waves in system, it is also the dimension of concentration space,
[OAc^-].......... concentration of OAc^- in water (mol/L of water),
[OAc_p].......... OAc^- concentration on parabola (mol/L of water),
[OAc].......... concentration of OAc^- on ion exchange resin (mol/L of system ("IX bed")),
[OH^-].......... concentration of OH^- in water (mol/L of water),
[OH].......... concentration of OH^- on ion exchange resin (mol/L of system ("IX bed")),
p.......... index assigned to point c_p = {[OAc_p^-], [Cl_p^-] on parabola,
√[].......... square root of the expression in [],
t.......... time variable (s),
u.......... superscript assigned to quantities referring to upper part of parabola,
v_w.......... flux of water (m³ of water per m² of flow channel cross section. Note: channels have tiny cross sections),
v_w/φ .......... speed of the water in the porous medium (m/s)
w_k.......... k-Riemann invariant (the invariant that changes across the k-rarefaction wave),
X_T.......... concentration of adsorbing sites on ion exchange resin (mol/L of system ("IX bed")),
x.......... spatial variable (m),
ξ, ξ(c).......... speed of concentration vector c (m/s),
-.......... subscript assigned to concentration at t = 0, x <= 0,
+.......... subscript assigned to concentration at t = 0, x > 0,
'.......... derivative with respect to ξ, meaning the change across the wave.

References

Gruber, J., Contaminant accumulation during transport through porous media, Water Resour. Res., 26, 99 - 107, 1990. (an enhanced version of my paper.)

Gruber, J., Waves in a two-component system: The oxide surface as a variable charge adsorbent, Ind. Eng. Chem. Res., 34, 2769-2781, 1995. (a modified version of my paper.)

Gruber, J. Advective transport of interacting solutes: the chromatographic model, in: U. Förstner and W. Calmano (eds.), "Sediments and Toxic Substances", Environmental Sciences Series, Springer, Heidelberg, 1996. (a modified version of my paper.)

Helfferich, F.G. and B.J. Bennett, Weak electrolytes, polybasic acids, and buffers in anion exchange columns: I. Sodium acetate and sodium carbonate systems, Reactive Polymers, 3, 51 - 66, 1984 a.

Helfferich, F.G. and B.J. Bennett, Weak electrolytes, polybasic acids, and buffers in anion exchange columns: II. Sodium acetate chloride system, Solvent Extraction and Ion Exchange, 2, 1151 - 1184, 1984 b.

Helfferich, F. and G. Klein, Multicomponent Chromatography - Theory of Interference, Marcel Dekker, New York, 1970. (out of print, available from University Microfilms, Ann Arbor, Michigan, USA)
Morel, F.M.M. and J.G. Hering, Principles and Applications of Aquatic Chemistry, John Wiley and Sons, New York, 1993.

Oelkers, E.H., Physical and chemical properties of rocks and fluids for chemical mass transport calculations, in: Reactive Transport in Porous Media, P.C. Lichtner, C.I. Steefel and E.H. Oelkers (eds.), Reviews in Mineralogy, 34, 131-191, 1996.

Rhee, H.-K., R. Aris and N.R. Amundson, First-Order Partial Differential Equations: Volume II, Theory and Application of Hyperbolic Systems of Quasilinear Equations, Prentice-Hall, Englewood Cliffs, New Jersey, NJ 07632, 1989.

Stumm, W. and J.J. Morgan, Aquatic Chemistry, 2nd ed., John Wiley, 1981.

Appendix: The Shape of Waves

How the adsorption stoichiometry determines the shapes of waves in 2-component systems.

Location of this page

last modified: December 15, 2013
Page compiled by Joachim Gruber